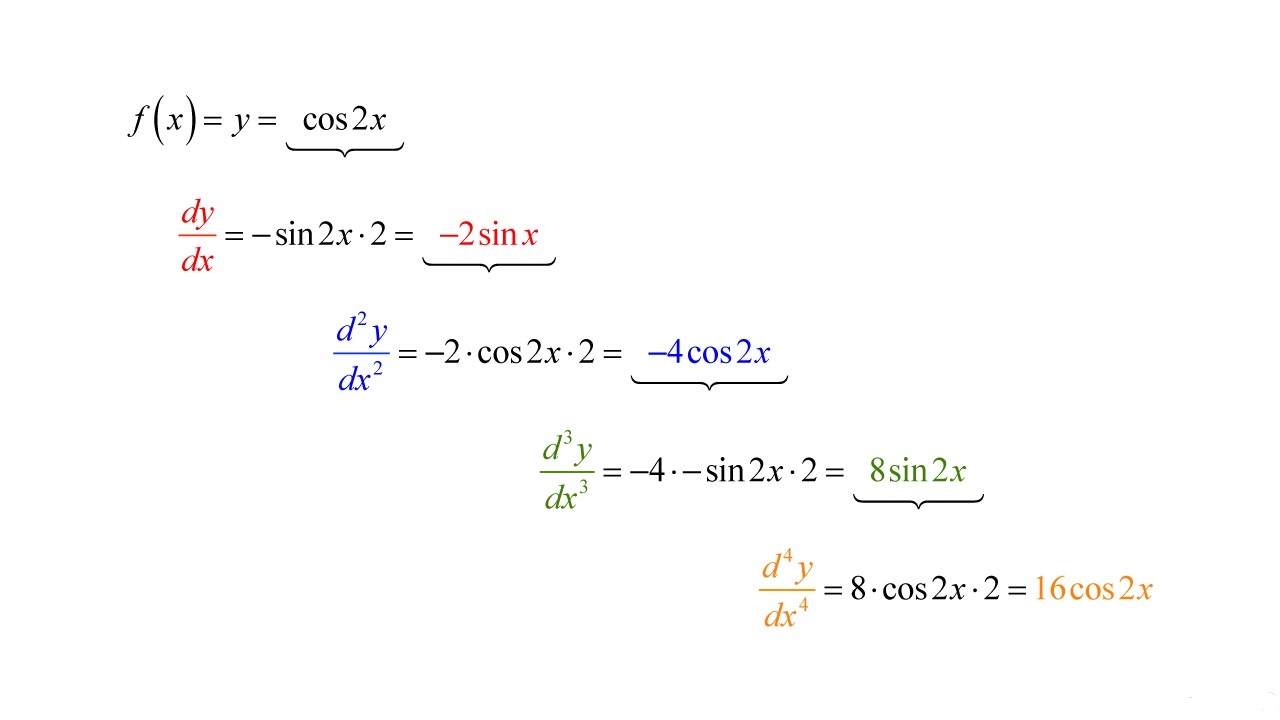How To Do Derivatives On TI-89

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for LiveWell, at no extra cost. Learn more)

Introduction

Welcome to the world of derivatives on the TI-89 calculator! Derivatives play a crucial role in calculus and have numerous applications in fields such as physics, engineering, economics, and finance. The ability to perform derivatives on the TI-89 calculator empowers users to solve complex problems with ease and efficiency.

In this article, we will guide you through the process of doing derivatives on the TI-89 calculator. Whether you are a student learning calculus or a professional working with mathematical models, this guide will help you unlock the power of derivatives on your calculator.

The TI-89 calculator is a versatile tool that not only performs basic arithmetic operations but also offers advanced mathematical functions. With its built-in calculus capabilities, the TI-89 allows you to find derivatives of functions, solve optimization problems, and even graph derivatives.

Understanding derivatives is essential for determining rates of change, analyzing curves, and optimizing functions. By mastering the techniques of doing derivatives on the TI-89 calculator, you can save time and gain a deeper understanding of calculus concepts. So, let’s dive in and explore how to unleash the full potential of derivatives on your TI-89!

Getting Started with the TI-89 Calculator

If you’re new to using the TI-89 calculator, don’t worry! We’ll walk you through the initial steps to get started on your derivative journey.

First, familiarize yourself with the layout and buttons of the TI-89 calculator. The calculator has a QWERTY keyboard, which makes it easy to enter equations and commands. Take some time to explore the different keys, including the arrow keys, function keys, and the math and calculus menus.

Next, let’s enter a function into the calculator. Press the “Y=” button to access the function editor. Here, you can input the equation you want to differentiate. Use the “X,T,θ,n” key to enter variables and the appropriate keys for mathematical operations.

Once you’ve entered the function, it’s time to find its derivative. You have two options: you can either use the calculator’s built-in derivative function or apply the basic derivative rules manually.

If you choose to use the built-in derivative function, press “2nd” followed by “8” to access the calculus menu. Here, you’ll find the “d/dx” function, which allows you to find the derivative of a function. Simply input the expression you want to differentiate, and the calculator will provide you with the result.

If you prefer to apply the basic derivative rules manually, make sure you have a good understanding of these rules first. The key rules include the power rule, product rule, quotient rule, chain rule, and trigonometric rules. To differentiate a function using these rules, input the expression into the function editor and follow the appropriate steps to apply the rule.

As you become more comfortable with the calculator, you can explore additional features like graphing derivatives, solving optimization problems, and finding higher-order derivatives.

That’s it! You’re now ready to start exploring the wonderful world of derivatives on the TI-89 calculator. The calculator’s powerful math capabilities will help you solve complex problems and gain a deeper understanding of calculus concepts. So, let’s roll up our sleeves and dive into the exciting realm of derivatives!

Understanding Derivatives

Before diving into the practical steps of doing derivatives on the TI-89 calculator, it’s important to have a solid understanding of what derivatives are and why they are crucial in calculus.

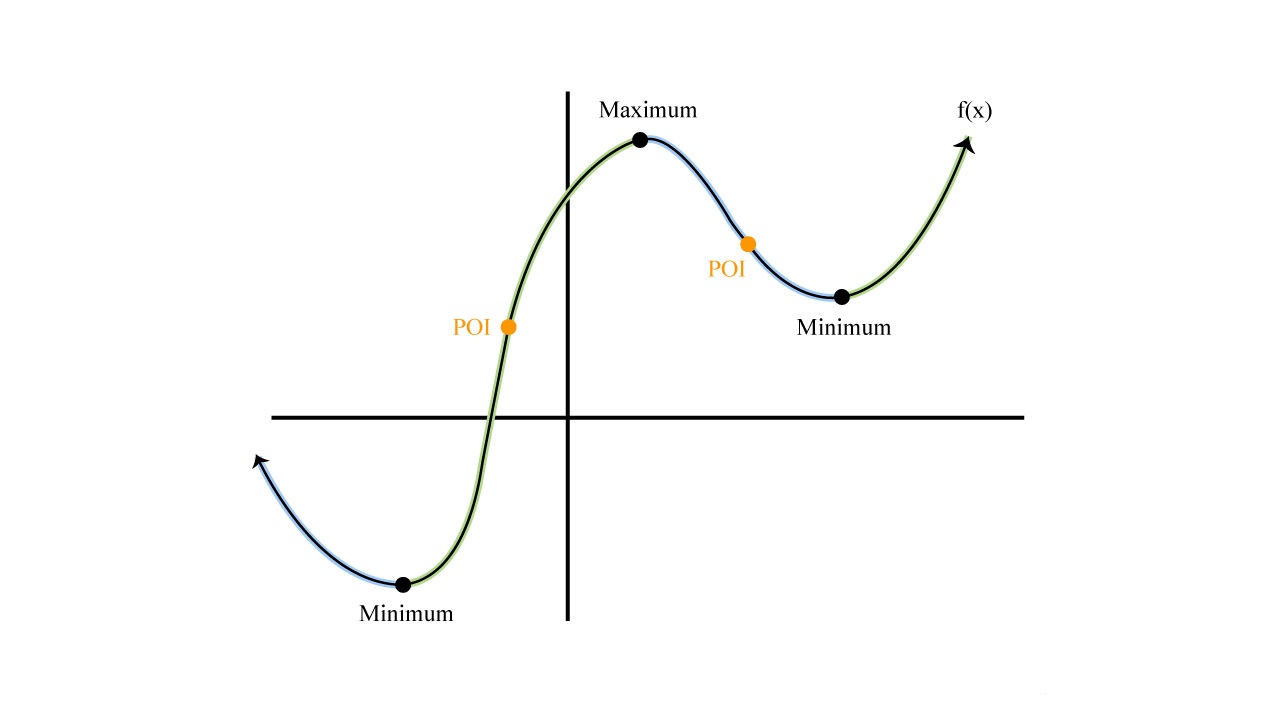
In calculus, a derivative measures the rate of change of a function at any given point. It tells us how the function is changing, whether it’s increasing or decreasing, and the slope of the tangent line at a specific point on the graph.

Graphically, the derivative represents the slope of the tangent line to the curve at a particular point. If the derivative is positive, the function is increasing, and if it’s negative, the function is decreasing. A derivative of zero indicates the function has a critical point.

Derivatives have a wide range of applications across various fields. In physics, derivatives help us analyze the motion of objects and determine velocities and accelerations. In economics and finance, derivatives are used to measure rates of change in variables such as prices, interest rates, and investment returns.

To understand the concept of derivatives, it’s important to grasp the concept of limits. The derivative of a function f(x) at a point x is defined as the limit of the difference quotient as the change in x approaches zero:

f'(x) = lim (Δx → 0) [f(x + Δx) – f(x)] / Δx

This formula expresses the instantaneous rate of change of the function at point x. It tells us how the function behaves at that particular point. The derivative provides valuable information about the behavior of functions, such as their slope and concavity.

By understanding the fundamental principles of derivatives and their applications, you’ll be ready to tackle more complex problems on the TI-89 calculator. So, let’s build a strong foundation and explore the basic derivative rules in the next section!

Basic Derivative Rules on the TI-89

When it comes to doing derivatives on the TI-89 calculator, having a strong grasp of the basic derivative rules is essential. These rules make it easier to differentiate functions and simplify the process of finding derivatives.

Here are some of the most commonly used basic derivative rules:

1. Power Rule: The power rule states that the derivative of a function raised to the power of a constant is equal to that constant multiplied by the function raised to the power of the constant minus one. For example, if we have the function f(x) = x^n, then its derivative, f'(x), is n*x^(n-1). The TI-89 calculator can handle various powers and constants, making it a handy tool for applying the power rule.
2. Product Rule: The product rule allows us to find the derivative of a function that is the product of two other functions. The rule states that the derivative of the product of two functions u(x) and v(x) is equal to u'(x)*v(x) + u(x)*v'(x). This rule is useful when dealing with functions that involve multiplication, such as polynomials or product terms.
3. Quotient Rule: The quotient rule is used when we need to find the derivative of a function that is the quotient of two other functions. If we have the function f(x) = u(x)/v(x), then its derivative, f'(x), is equal to (u'(x)*v(x) – u(x)*v'(x))/(v(x))^2. The quotient rule comes in handy when working with fractions or when dealing with rational functions.
4. Chain Rule: The chain rule allows us to find the derivative of a composition of functions. If we have the function f(g(x)), where g(x) is a function of x, and f(x) is a function of g(x), then the derivative of f(g(x)) is equal to f'(g(x))*g'(x). This rule is particularly useful when dealing with composite functions, such as trigonometric functions or exponential functions nested inside other functions.

The TI-89 calculator has built-in functions to handle these basic derivative rules. By applying the appropriate rule to a given function, you can quickly find its derivative using the calculator’s powerful math capabilities.

By mastering these basic derivative rules, you’ll be well-equipped to differentiate a wide range of functions on the TI-89 calculator. In the next section, we’ll explore how to use the calculator’s derivative function to find derivatives more efficiently. So, let’s continue our derivative journey!

Using the Calculator’s Derivative Function

The TI-89 calculator offers a built-in derivative function that allows you to find the derivative of a function with just a few button presses. This function simplifies the process of differentiating functions, especially when dealing with complex equations.

To access the calculator’s derivative function, press “2nd” followed by “8” to access the calculus menu. Here, you’ll find the “d/dx” function, which is used to find the derivative of a function.

To use the “d/dx” function, follow these steps:

1. Enter the function whose derivative you want to find into the calculator’s function editor. Press the “Y=” button and input the equation using the appropriate keys and functions.
2. After entering the function, move the cursor to the function you want to differentiate. Highlight the function by using the arrow keys.
3. Press “ENTER” to select the function.
4. Finally, press “d/dx” to calculate the derivative. The calculator will display the derivative of the function.

The TI-89 calculator can handle a wide range of functions, including polynomials, exponential functions, logarithmic functions, and trigonometric functions. It can even differentiate more complex expressions involving multiple variables and constants.

The “d/dx” function allows you to find both first-order and higher-order derivatives. Once you have calculated the derivative of a function, you can continue to differentiate it further by using the “d/dx” function repeatedly.

Using the calculator’s derivative function saves time and simplifies the process of finding derivatives, especially when dealing with complex equations or higher-order derivatives. It is a powerful tool that enhances productivity and helps in gaining a deeper understanding of calculus concepts.

In the next section, we’ll explore how to find derivatives of trigonometric functions on the TI-89 calculator. So, let’s continue our exploration of derivatives!

Finding Derivatives of Trigonometric Functions

Trigonometric functions, such as sine, cosine, and tangent, are commonly encountered in mathematical problems. Knowing how to find their derivatives is essential for solving calculus problems involving trigonometry. The TI-89 calculator provides a straightforward way to find the derivatives of trigonometric functions.

Here’s how you can find the derivatives of trigonometric functions on the TI-89:

1. Sine Function: To find the derivative of the sine function, enter “sin(x)” into the calculator’s function editor. Use “x” as the variable. Then press “d/dx” to calculate the derivative. The calculator will display “cos(x)”, which is the derivative of the sine function.
2. Cosine Function: For the derivative of the cosine function, enter “cos(x)” into the function editor and press “d/dx”. The calculator will show “-sin(x)” as the derivative of the cosine function.
3. Tangent Function: To find the derivative of the tangent function, enter “tan(x)” into the function editor and press “d/dx”. The calculator will give “sec^2(x)” as the derivative of the tangent function.
4. Other Trigonometric Functions: The TI-89 calculator also provides derivatives for other trigonometric functions, such as cotangent, secant, and cosecant. To find their derivatives, simply enter the corresponding function into the function editor and press “d/dx” to calculate the derivative.

It’s important to note that the TI-89 calculator assumes the input is in radians unless specified otherwise. If you’re working with degrees, make sure to convert the angles to radians before finding the derivatives.

With the TI-89 calculator’s ability to quickly find derivatives of trigonometric functions, you can efficiently solve problems involving angles, periodicity, and trigonometric relationships. The calculator’s accuracy and speed make it a valuable tool for trigonometry and calculus courses.

Next, we’ll explore the application of the chain rule on the TI-89 calculator, which allows us to find the derivatives of composite functions. So, let’s continue our exploration of derivatives!

Applying the Chain Rule on the TI-89

The chain rule is a fundamental concept in calculus that allows us to find the derivative of composite functions. When we have a function nested inside another function, the chain rule gives us a method to differentiate the composition. With the TI-89 calculator, applying the chain rule becomes a breeze.

Here’s how you can apply the chain rule on the TI-89:

1. Enter the composite function into the calculator’s function editor. Make sure to use the appropriate syntax and parentheses to indicate the composition of functions.
2. Press the “d/dx” button to indicate that you want to find the derivative with respect to x.
3. The TI-89 will prompt you to enter the inner function, f(g(x)). Enter the inner function and press “ENTER”.
4. The calculator will then ask for the derivative of the inner function, f'(g(x)). Enter the derivative and press “ENTER”.
5. Finally, the TI-89 will display the derivative of the composite function using the chain rule.

The beauty of the chain rule lies in its ability to handle complex functions with multiple layers of composition. Whether you’re working with exponential functions, logarithmic functions, trigonometric functions, or any combination thereof, the TI-89 calculator can effortlessly find the derivatives using the chain rule.

By applying the chain rule on the TI-89, you can efficiently find the derivatives of composite functions, allowing you to solve more complicated calculus problems. It’s a powerful tool that greatly simplifies the process of differentiation and saves valuable time.

In the next section, we’ll explore how to solve optimization problems using derivatives on the TI-89 calculator. So, let’s continue our journey through the world of derivatives!

Solving Optimization Problems with Derivatives on the TI-89

Optimization problems involve finding the maximum or minimum value of a function within a given range. Derivatives play a crucial role in solving these types of problems, and the TI-89 calculator is a valuable tool for finding the optimal solutions.

Here’s how you can use derivatives on the TI-89 to solve optimization problems:

1. Start by defining the function that represents the quantity you want to optimize. This could be a cost function, revenue function, or any other function related to the problem at hand.
2. Next, determine the range or constraints within which you need to find the maximum or minimum value. This could be given in terms of equations, inequalities, or specific conditions.
3. Using the derivative function on the TI-89, find the derivative of the objective function.
4. Set the derivative equal to zero and solve for the critical points. These critical points are the potential locations of maximum or minimum values.
5. Evaluate the objective function at the critical points as well as at the endpoints of the given range.
6. Compare the values obtained in the previous step to determine the maximum or minimum value and its location within the given range. This involves considering factors such as the sign of the derivative, the concavity of the function, and the constraints of the problem.

The TI-89 calculator with its advanced math capabilities can handle complex objective functions and efficiently find the derivatives required for solving optimization problems. It provides a fast and accurate way to determine the optimal solutions.

Solving optimization problems using derivatives on the TI-89 can be especially useful in fields such as economics, engineering, and physics. It allows you to make informed decisions by maximizing or minimizing certain variables based on specific constraints or criteria.

It’s important to note that while the TI-89 can perform the calculus calculations for optimization problems, understanding the concepts behind optimization and interpreting the results are crucial. Make sure to double-check your work and consider the context of the problem to ensure the solutions make sense.

In the next section, we’ll explore how to graph derivatives on the TI-89, which helps visualize the behavior of functions and their rates of change. So, let’s continue our journey through the world of derivatives!

Graphing Derivatives on the TI-89

The TI-89 calculator not only allows you to find derivatives but also enables you to graph them. Graphing derivatives can provide valuable insights into the behavior of functions and their rates of change. The TI-89’s graphing capabilities make it easy to visualize these relationships.

Here’s how you can graph derivatives on the TI-89:

1. Enter the function whose derivative you want to graph into the calculator’s function editor. This function will serve as the base function.
2. Use the “d/dx” function to find the derivative of the base function. The calculator will display the derivative as a separate function.
3. Press the “Y=” button to access the graphing menu. Enter both the base function and the derivative function into the Y= editor. You can assign different colors or line styles to each function for easier differentiation.
4. Adjust the window settings in the graphing menu to ensure the entire function and its derivative are visible on the graph. You may need to adjust the x-range, y-range, and scale to achieve a clear representation.
5. Once the settings are adjusted, press the “GRAPH” button, and the TI-89 will plot the graph of both the base function and its derivative on the same coordinate plane.

By graphing derivatives, you can visually analyze the slopes, maxima, minima, and inflection points of a function. The graph provides a clear representation of the behavior of the function and its rate of change at different points.

The TI-89 calculator’s graphing capabilities allow you to explore complex functions and their derivatives, enabling a deeper understanding of calculus concepts. You can also compare the graph of the base function to its derivative to observe the relationship between the two.

Graphing derivatives on the TI-89 is a powerful tool that can assist in analyzing functions, optimizing solutions, and gaining a visual intuition of calculus concepts. It enhances your ability to interpret and visualize mathematical relationships.

Now that we have explored how to graph derivatives on the TI-89, let’s wrap up our journey through the world of derivatives in the next section.

Conclusion

Congratulations! You have completed your journey through the world of derivatives on the TI-89 calculator. We explored how to get started with the calculator, understand derivatives, apply basic derivative rules, use the calculator’s derivative function, find derivatives of trigonometric functions, apply the chain rule, solve optimization problems, and graph derivatives.

The TI-89 calculator proved to be an invaluable tool for performing derivatives efficiently and accurately. Its built-in functions and user-friendly interface allowed us to tackle complex calculus problems with ease.

Derivatives play a crucial role in calculus and have wide-ranging applications in various fields of study. By mastering the techniques of doing derivatives on the TI-89 calculator, you have equipped yourself with a powerful skill that can aid in solving real-world problems, optimizing solutions, and gaining insights into the behavior of functions.

Remember, practice makes perfect. The more you use the TI-89 calculator and apply the concepts of derivatives, the more confident you will become in your ability to handle calculus problems. Continuously exploring new functions, differentiating various types of equations, and solving diverse optimization problems will expand your knowledge and deepen your understanding of calculus.

Whether you’re a student learning calculus or a professional working with mathematical models, the ability to perform derivatives on the TI-89 calculator will bring you one step closer to mastering the subject and achieving your goals.

So, keep exploring, keep learning, and keep leveraging the power of derivatives on the TI-89 calculator. The journey doesn’t end here – there are always new concepts, new equations, and new challenges to tackle. Embrace the world of derivatives and see where it takes you!