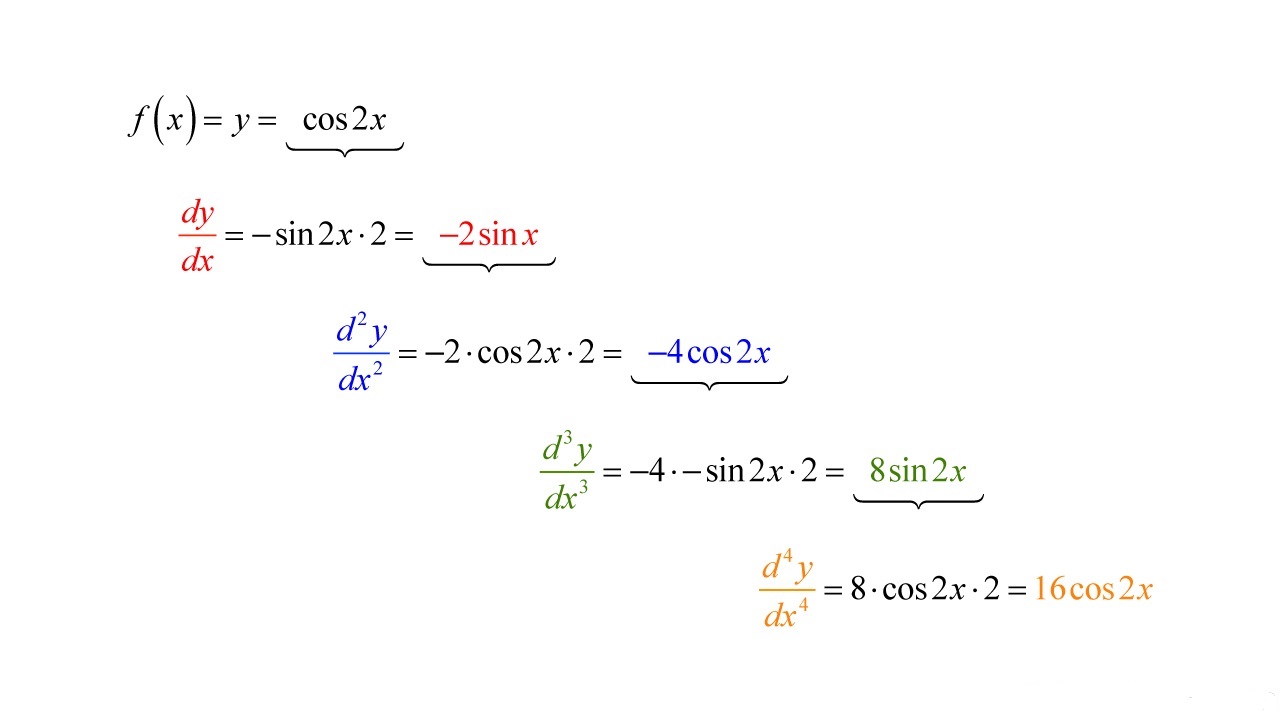

Finance
How To Graph Derivatives
Published: October 5, 2023
Learn how to graph derivatives in finance and make informed decisions with this comprehensive guide. Enhance your understanding of finance derivatives and their applications.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for LiveWell, at no extra cost. Learn more)
Table of Contents
Introduction
Welcome to this comprehensive guide on how to graph derivatives. If you’re familiar with calculus and have a basic understanding of derivatives, this article will help you enhance your knowledge and graphing skills.
Derivatives are a fundamental concept in calculus and have numerous applications in various fields, including finance, physics, engineering, and more. Graphing derivatives allows us to visualize and analyze the rate of change of a function, providing valuable insights into its behavior.
Understanding how to graph derivatives is essential for optimizing functions, identifying critical points, finding maximum and minimum values, and determining the concavity of a function. By visually representing the derivative of a function, we gain a deeper understanding of its properties and can make informed decisions based on the information provided by the graph.
This guide will walk you through the core concepts of graphing derivatives, starting with a brief overview of derivatives and their importance. We will then delve into the differentiation rules that enable us to calculate derivatives efficiently. From there, we will explore different graphing techniques to visually represent derivatives and study their characteristics.
Examples illustrating the process of graphing derivatives will be provided throughout the article, allowing you to practice and apply the concepts explained. By the end of this guide, you will have the knowledge and skills necessary to confidently graph derivatives and analyze the behavior of functions.
So, whether you’re a student looking to deepen your understanding of calculus, a finance professional wanting to optimize investment strategies, or simply someone interested in exploring the world of derivatives, this article will equip you with the techniques and tools needed to graph derivatives effectively.
Are you ready to dive into the fascinating world of graphing derivatives? Let’s get started!
Understanding Derivatives
In order to effectively graph derivatives, it is crucial to have a solid understanding of what derivatives are and how they relate to functions. Derivatives measure the rate at which a function is changing at a specific point, providing valuable information about its behavior.
A derivative represents the slope of a function at a particular point. It tells us how the function is changing in relation to the independent variable. If the derivative is positive, it means the function is increasing. If the derivative is negative, the function is decreasing. Zero derivative indicates a stationary point where the function is neither increasing nor decreasing.
Derivatives have several interpretations, such as the instantaneous rate of change, the slope of the tangent line to the curve, or the velocity of an object. In finance, derivatives are used to measure risk, calculate options prices, and manage portfolio strategies.
The derivative of a function f(x) is typically denoted as f'(x) or dy/dx. It is calculated using the rules of differentiation, which allow us to find the derivative of various types of functions. These rules include the power rule, product rule, quotient rule, and chain rule.
In addition to the rules of differentiation, it is essential to understand the concept of continuity when working with derivatives. A function is said to be continuous if there are no breaks or jumps in its graph. Continuous functions have derivatives at every point within their domain, allowing for the smooth calculation and graphing of derivatives.
Graphing derivatives provides valuable insights into the behavior of functions. It allows us to identify critical points, such as maximum and minimum values, and understand the concavity of a function. Concavity refers to the curvature of a function’s graph and can be determined by examining the second derivative.
Overall, understanding derivatives is key to effectively graphing them. By grasping the concept of derivatives, their interpretations, and the rules of differentiation, you will be well-equipped to analyze functions and make informed decisions based on their behavior. Now that we have a solid understanding of derivatives, let’s explore the rules of differentiation in the next section.
Differentiation Rules
When graphing derivatives, it is essential to have knowledge of the differentiation rules that allow us to calculate derivatives efficiently. These rules provide shortcuts and formulas for finding the derivative of various types of functions.
The power rule is one of the most basic and commonly used rules of differentiation. It states that if f(x) = x^n, where n is a constant, then the derivative of f(x) is given by f'(x) = nx^(n-1). This rule allows us to find the derivative of polynomials, such as quadratic, cubic, and higher-order functions.
The product rule is used when we need to differentiate the product of two functions. If f(x) = g(x) * h(x), then the derivative of f(x) can be found using the formula f'(x) = g'(x) * h(x) + g(x) * h'(x). This rule is particularly useful when dealing with expressions that involve multiple functions multiplied together.
The quotient rule is employed when we need to differentiate the quotient of two functions. If f(x) = g(x) / h(x), then the derivative of f(x) can be determined using the formula f'(x) = (g'(x) * h(x) – g(x) * h'(x)) / h(x)^2. This rule allows us to find the derivative of expressions involving fractions or divisions.
The chain rule is used when we have a composition of functions, where one function is inside another. If f(x) = g(h(x)), then the derivative of f(x) can be obtained by taking the derivative of the outer function multiplied by the derivative of the inner function. Symbolically, this is written as f'(x) = g'(h(x)) * h'(x). The chain rule allows us to differentiate complex functions more easily.
In addition to these fundamental rules, there are several other rules of differentiation, such as the sum and difference rules, the constant rule, and the logarithmic and exponential rules. Each rule provides a specific formula or procedure for finding the derivative of a given function.
Having a solid understanding of these differentiation rules is crucial for graphing derivatives effectively. By being able to quickly and accurately calculate the derivative of a function, we can graph it and analyze its behavior more efficiently. In the next section, we will explore various graphing techniques specifically designed for derivatives.
Graphing Techniques for Derivatives
Graphing derivatives provides valuable insights into the behavior of functions and allows us to visualize their rate of change. There are several techniques that can be employed to graph derivatives effectively and understand their characteristics.
One common technique is to plot the derivative function on the same graph as the original function. This allows us to directly compare the behavior of the original function with its derivative. For example, if the derivative is positive in a certain interval, it indicates that the original function is increasing in that interval. If the derivative is negative, the function is decreasing.
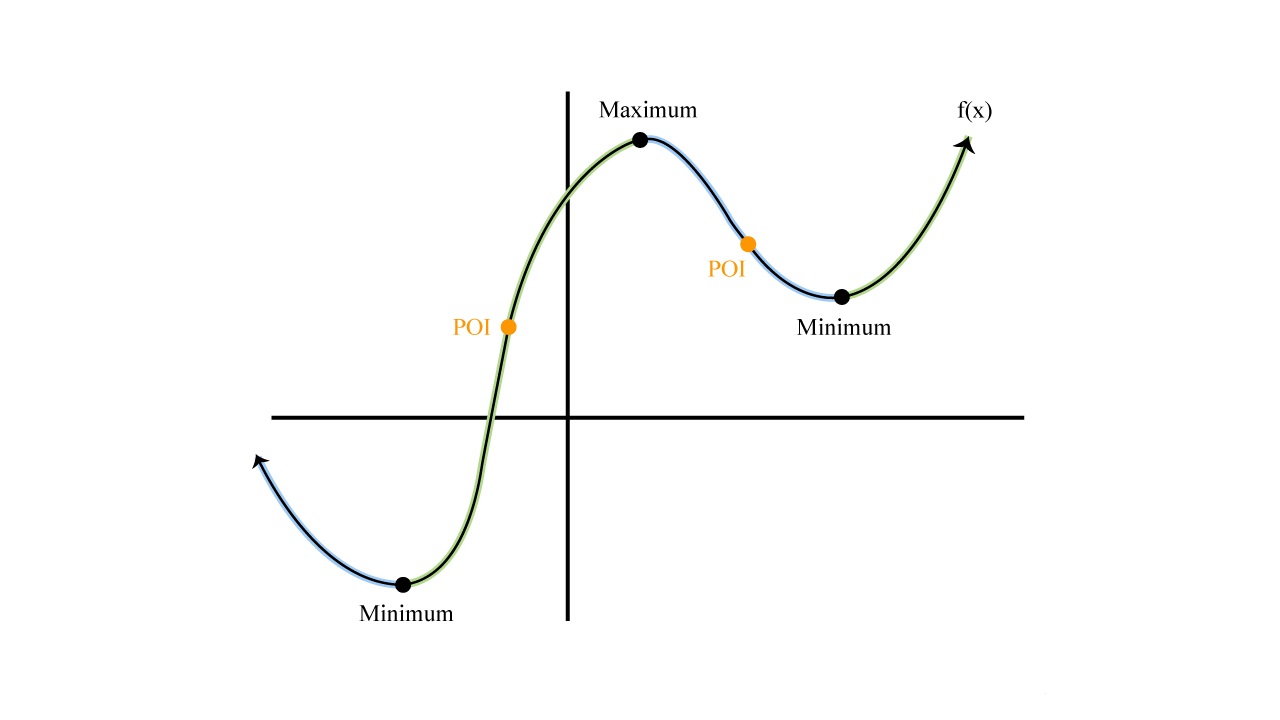
Interpreting the sign of the derivative is often useful for identifying critical points, such as local maximum and minimum values. A local maximum occurs when the derivative changes from positive to negative, indicating a peak in the original function. A local minimum occurs when the derivative changes from negative to positive, indicating a valley.
The concavity of a function, which refers to its curvature, can also be visualized through the graph of its second derivative. The second derivative provides information about how the rate of change of the original function is changing. If the second derivative is positive, the function is concave up, meaning it looks like a U-shaped curve. If the second derivative is negative, the function is concave down, resembling an inverted U.
Another technique for graphing derivatives is to use the concept of critical points. Critical points occur when the derivative of a function is either zero or undefined. These points can indicate locations where the function has a maximum, minimum, or an inflection point.
Inflection points are points where the concavity of the function changes. They are identified by examining the change in sign of the second derivative. By graphing the second derivative, we can visually identify and analyze the behavior of inflection points.
Graphing techniques for derivatives also involve considering the behavior of the original function at the boundaries of its domain. By examining the limits of the function as it approaches positive and negative infinity, we can gain insights into the end behavior of the function and its derivative.
Overall, graphing techniques for derivatives involve visualizing the derivative function, interpreting its sign, identifying critical points, analyzing concavity, and considering the behavior of the original function. These techniques allow us to gain a deeper understanding of the behavior and characteristics of functions, making them valuable tools in calculus and real-world applications.
Examples of Graphing Derivatives
Let’s explore some examples to illustrate the process of graphing derivatives and how it can provide insights into the behavior of functions.
Example 1: Consider the function f(x) = x^2. To graph its derivative, we first apply the power rule, which gives us f'(x) = 2x. The derivative is a linear function with a slope of 2 at every point. This means that the original function f(x) is increasing at a constant rate. The graph of the derivative will be a straight line with positive slope, indicating that the original function is concave up.
Example 2: Let’s take the function g(x) = sin(x). Its derivative can be found using the chain rule: g'(x) = cos(x). The derivative of a sine function is a cosine function. The graph of the derivative, cos(x), oscillates between -1 and 1 as x changes. This indicates that the original function g(x), which represents a periodic oscillation, has maximum and minimum points at different intervals.
Example 3: Consider the function h(x) = x^3 – 3x^2 + 2x. To graph its derivative, we can use the power rule for each term: h'(x) = 3x^2 – 6x + 2. The graph of the derivative is a quadratic function. By examining the sign of the derivative, we can identify critical points and determine the intervals where the original function h(x) is increasing or decreasing.
Example 4: Let’s take the function j(x) = e^x. Its derivative, j'(x), is equal to e^x as well. The graph of the derivative is an exponential function that increases rapidly as x grows. This indicates that the original function j(x), which represents exponential growth, is increasing at an accelerating rate.
These examples demonstrate how graphing derivatives can provide valuable information about the behavior of functions. By analyzing the slope, sign, and concavity of the derivative, we can determine key characteristics such as increasing/decreasing intervals, maximum/minimum points, and the overall shape of the function.
It is worth noting that graphing software and calculators can be powerful tools for visualizing derivatives and their corresponding functions. They allow for a more precise representation and a deeper exploration of their properties.
Now that we have seen some examples of graphing derivatives, let’s move on to the concluding section to summarize the key points and highlight the importance of this technique in calculus and beyond.
Conclusion
Graphing derivatives is a fundamental skill in calculus that allows us to visually analyze the behavior of functions. By understanding the concept of derivatives, applying differentiation rules, and employing graphing techniques, we can gain valuable insights into the rate of change, concavity, and critical points of functions.
The process of graphing derivatives involves plotting the derivative function on the same graph as the original function, interpreting the sign of the derivative to determine increasing or decreasing intervals, and analyzing the concavity of the function using the second derivative.
By graphing derivatives, we can identify important features of functions such as maximum and minimum points, inflection points, and overall shape. This information is valuable in various fields, including finance, where optimizing investment strategies relies on understanding the behavior of financial models.
Utilizing graphing technology, calculators, and software further enhances the accuracy and efficiency of graphing derivatives, allowing for a more in-depth exploration of functions and their characteristics.
In conclusion, graphing derivatives is a powerful tool in calculus and mathematics that aids in the interpretation and analysis of functions. It provides visual representations that help us understand the rate of change, concavity, and critical points of functions. By mastering the techniques of graphing derivatives, we can make informed decisions and solve problems in a wide range of domains. So, embrace the fascinating world of graphing derivatives and unlock the insights it offers for a deeper understanding of functions and their behavior.