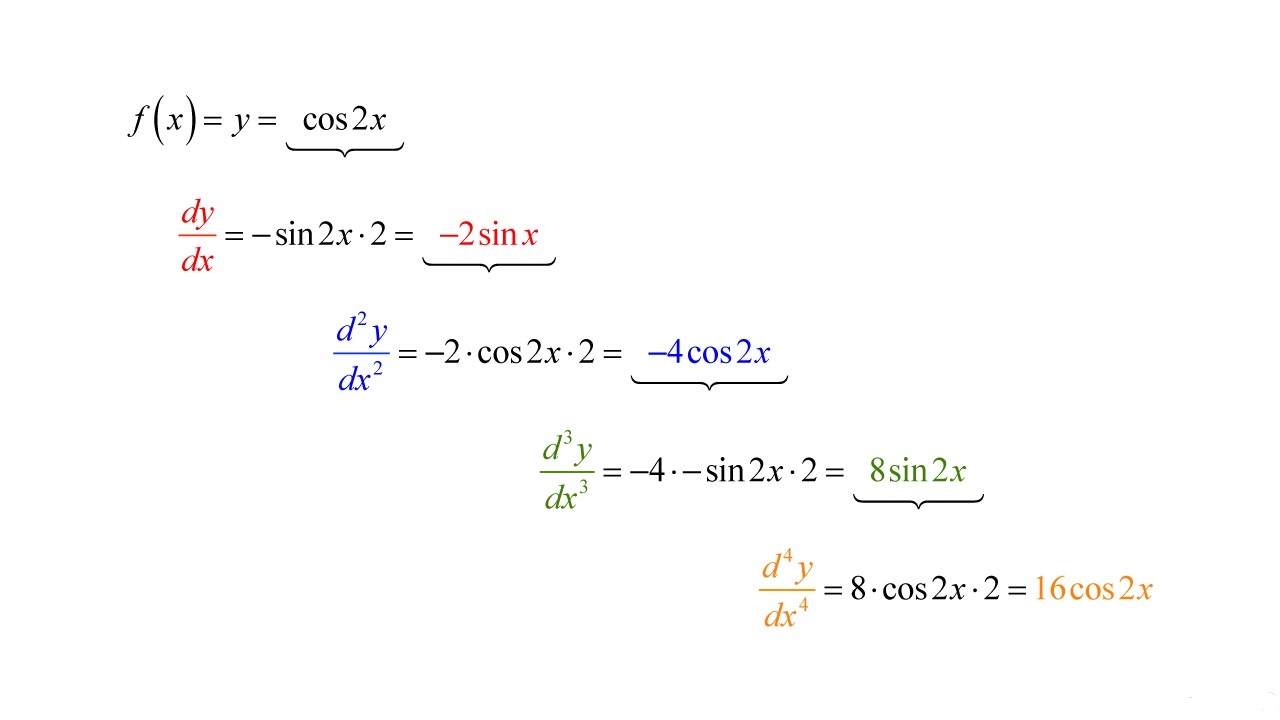Finance
How To Calculate Derivatives In Matlab
Published: October 6, 2023
Learn how to calculate derivatives in Matlab for finance applications. Improve your financial analysis skills with step-by-step instructions and examples.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for LiveWell, at no extra cost. Learn more)
Table of Contents
Introduction
When it comes to financial analysis and decision-making, it is crucial to have a deep understanding of the underlying mathematical concepts. One such concept that is widely used in finance is derivatives. Derivatives allow us to analyze and measure the rate of change of a quantity with respect to another.
In simple terms, derivatives can be understood as the slope of a curve at a specific point. They provide valuable insights into the behavior and characteristics of a financial instrument or investment. By calculating derivatives, we can determine how sensitive certain variables are to changes in others, enabling us to make informed decisions.
In the world of finance, many professionals and researchers rely on programming languages like Matlab to perform complex calculations and analysis. Matlab offers a comprehensive set of tools and functions that make it ideal for working with derivatives and other mathematical concepts.
This article aims to provide a comprehensive guide on how to calculate derivatives using Matlab. We will cover both symbolic differentiation, which involves computing derivatives analytically, and numeric differentiation, which involves approximating derivatives using numerical methods.
By the end of this article, you will have a solid understanding of how to leverage Matlab to calculate derivatives efficiently, giving you a valuable tool in your financial analysis toolkit.
Understanding Derivatives
Before diving into the details of calculating derivatives in Matlab, it’s important to have a clear understanding of what derivatives are and why they are essential in finance.
Derivatives allow us to measure the rate of change of a quantity with respect to another. In the context of finance, derivatives are used to assess the sensitivity of financial instruments, such as options, futures contracts, and swaps, to changes in underlying variables.
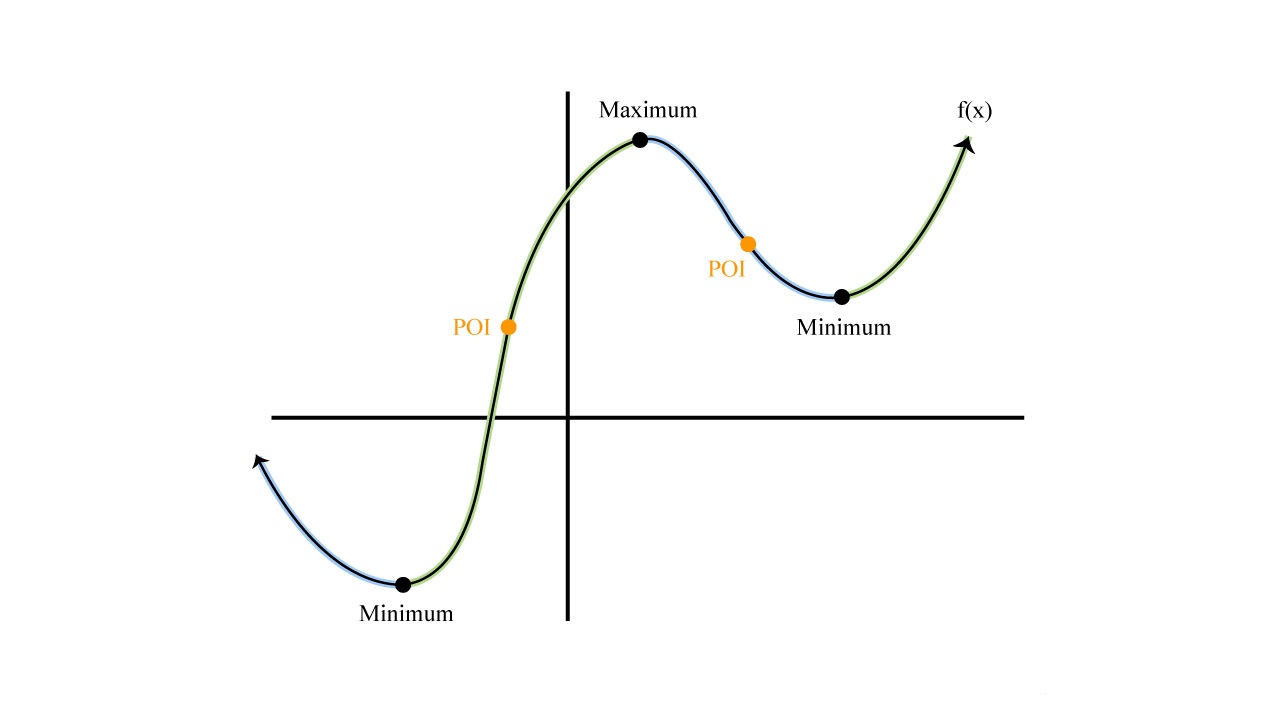
The concept of a derivative is closely related to the idea of a slope. Imagine a graph that represents the relationship between two variables, such as time and the value of a stock. The derivative at a specific point on the graph reflects how fast the stock price is changing at that moment. A positive derivative indicates an increasing trend, while a negative derivative signifies a decreasing trend.
Derivatives are widely used in finance to evaluate risk and make informed investment decisions. For example, the delta of an option measures the rate at which the option price changes with respect to the underlying asset’s price. This helps traders assess the sensitivity of their options positions to changes in the market.
Additionally, derivatives play a crucial role in financial modeling and pricing. By understanding the derivatives of various financial instruments, analysts can build sophisticated models that capture the complex dynamics of the market. These models are then used to estimate the fair value of derivatives and assess the risk associated with them.
Overall, derivatives are an essential tool in the world of finance. They provide valuable insights into the behavior of financial instruments, help quantify risk, and enable informed decision-making.
Derivatives in Matlab
Matlab is a powerful programming language and environment that offers a wide range of tools for numerical computation and analysis. It provides convenient functions for calculating derivatives, making it a popular choice for financial professionals and researchers.
In Matlab, there are two main ways to calculate derivatives: symbolic differentiation and numeric differentiation.
Symbolic Differentiation: Symbolic differentiation involves computing derivatives analytically, using mathematical rules and formulas. Matlab’s Symbolic Math Toolbox allows you to work with symbolic variables and perform symbolic operations, including differentiation. This approach is useful when you want to obtain exact symbolic expressions for derivatives, which can be helpful for further manipulation or analysis.
Numeric Differentiation: Numeric differentiation, on the other hand, involves approximating derivatives using numerical methods. Matlab provides various functions for numerical differentiation, such as diff and gradient. This approach is useful when you have numerical data and want to estimate the derivatives at specific points.
Both symbolic and numeric differentiation have their advantages and use cases. Symbolic differentiation is more precise and allows for symbolic manipulation of derivatives. On the other hand, numeric differentiation is faster and more suitable for handling large datasets or complex functions.
Matlab also offers additional functionalities for working with derivatives, such as integrating differential equations and optimizing functions using derivatives. These capabilities make Matlab a comprehensive tool for tackling a wide range of financial problems that involve derivatives.
Next, we will explore how to use these differentiation methods in Matlab to calculate derivatives efficiently.
Symbolic Differentiation in Matlab
Symbolic differentiation is the process of computing derivatives analytically using mathematical rules and formulas. Matlab’s Symbolic Math Toolbox provides a powerful set of functions for symbolic manipulation and differentiation. Let’s explore how to perform symbolic differentiation in Matlab.
First, we need to define the symbolic variables that we will be working with. Matlab allows us to create symbolic variables using the sym function. For example, to define a symbolic variable x, we can use the following code:
matlab
syms x
Once we have defined the symbolic variables, we can use the built-in symbolic functions to perform operations and calculate derivatives. The most commonly used function for symbolic differentiation is diff. This function takes the derivative of an expression with respect to a specified variable.
For example, let’s say we have an expression f(x) = x^2 + 3x - 2. To calculate the derivative of f(x) with respect to x, we can use the following code:
matlab
syms x
f = x^2 + 3*x – 2;
df = diff(f, x);
The variable df now stores the symbolic expression of the derivative f'(x). We can evaluate this expression at specific values of x using the subs function. For example, to evaluate the derivative at x = 2, we can use the following code:
matlab
df_value = subs(df, x, 2);
Symbolic differentiation in Matlab allows us to obtain exact symbolic expressions for derivatives, which can be useful for further manipulation or analysis. We can simplify the resulting expressions using the simplify function to obtain a more compact representation.
In addition to the diff function, Matlab’s Symbolic Math Toolbox provides various other functions for symbolic manipulation and differentiation, such as int for symbolic integration and limit for computing limits.
Symbolic differentiation in Matlab is a powerful tool that allows us to calculate derivatives analytically and obtain exact symbolic expressions. This approach is particularly useful when we want to perform further symbolic operations or analyze the properties of the derivatives.
Numeric Differentiation in Matlab
Numeric differentiation is the process of approximating derivatives using numerical methods. Matlab provides various functions for numeric differentiation, which are useful when we have numerical data or when symbolic differentiation is not feasible or efficient.
The most commonly used functions for numeric differentiation in Matlab are diff and gradient. The diff function calculates the difference quotient, which is an approximation of the derivative using finite differences. It takes the form (f(x + h) - f(x)) / h, where h is a small step size.
To use the diff function, we need a vector of values representing data points. For example, let’s say we have a vector x and another vector y representing the values of a function at different points. We can calculate the derivative of y with respect to x using the following code:
matlab
dy_dx = diff(y) ./ diff(x);
The resulting vector dy_dx contains the approximated derivatives at each point.
Another useful function for numeric differentiation in Matlab is gradient. The gradient function computes the gradient, or the vector of partial derivatives, of a function at each point. This is particularly useful when dealing with multivariable functions.
Similar to diff, the gradient function requires numerical data points. We can calculate the gradient of a function f using the following code:
matlab
[gx, gy] = gradient(f, x, y);
The resulting vectors gx and gy contain the approximated partial derivatives with respect to x and y, respectively.
It is important to note that numeric differentiation involves approximations and can introduce errors, especially when using small step sizes. Therefore, it is necessary to choose an appropriate step size to balance accuracy and computational efficiency.
Matlab also offers other advanced techniques for numeric differentiation, such as higher-order finite difference methods and spline interpolation. These methods can provide more accurate results by reducing the error introduced by finite differences.
Numeric differentiation in Matlab is a useful tool when dealing with numerical data or situations where symbolic differentiation is not feasible. By approximating derivatives, we can still gain valuable insights into the rate of change of a function without relying on exact mathematical formulas.
Example: Calculating Derivatives of a Function in Matlab
To illustrate the process of calculating derivatives in Matlab, let’s consider an example where we have a function and we want to calculate its derivatives at specific points.
Suppose we have the function f(x) = sin(x^2) and we want to calculate its derivative at the point x = 1. We can use Matlab to perform this calculation.
First, we define the symbolic variable x and the function f(x) using the sym function:
matlab
syms x
f = sin(x^2);
Next, we calculate the derivative of f(x) with respect to x using the diff function:
matlab
df = diff(f, x);
We now have the symbolic expression for the derivative of f(x). To evaluate the derivative at x = 1, we use the subs function:
matlab
df_value = subs(df, x, 1);
The variable df_value now holds the numerical value of the derivative at x = 1. In this case, the result is approximately -0.5403.
This example showcases how we can use Matlab to calculate derivatives of a function accurately and efficiently. By leveraging the symbolic differentiation capabilities of Matlab, we can obtain exact symbolic expressions for the derivatives and evaluate them at specific points to obtain numerical results.
It’s important to note that this is just a simple example, and Matlab provides much more advanced functionalities for working with derivatives, such as handling multivariable functions, integrating differential equations, and optimizing functions using derivatives.
By using Matlab’s powerful mathematical capabilities, you can perform sophisticated financial analysis and make informed decisions based on accurate calculations of derivatives.
Conclusion
Derivatives play a crucial role in finance, allowing us to measure the rate of change of a quantity with respect to another. By understanding derivatives and knowing how to calculate them, financial professionals can gain valuable insights into the behavior of financial instruments, assess risk, and make informed investment decisions.
Matlab provides a comprehensive set of tools for working with derivatives, making it a popular choice among financial professionals and researchers. By leveraging Matlab’s capabilities in symbolic differentiation and numeric differentiation, users can efficiently calculate derivatives of functions and analyze their properties.
In this article, we explored the process of calculating derivatives in Matlab. We covered both symbolic differentiation and numeric differentiation methods, highlighting their advantages and use cases. Symbolic differentiation allows for precise and exact symbolic expressions, while numeric differentiation provides quick and efficient approximations.
We also demonstrated how to calculate derivatives of a function using Matlab, following an example of a specific function. By defining symbolic variables, applying differentiation functions, and evaluating the derivatives at specific points, we can obtain accurate numerical results.
Ultimately, Matlab’s capabilities in calculating derivatives make it a powerful tool for financial analysis, modeling, and decision-making. Whether you are an analyst, trader, or researcher, knowing how to use Matlab for derivatives can enhance your analytical abilities and give you a competitive edge in the finance industry.
Remember, derivatives are not solely limited to finance. They have wide-ranging applications in various disciplines such as physics, engineering, and data analysis. Having a solid understanding of derivatives and being proficient in their calculations using Matlab can open up new possibilities and empower you to solve complex problems.
So, explore the world of derivatives, harness the power of Matlab, and embrace the opportunities that arise from mastering this fundamental and practical mathematical concept.