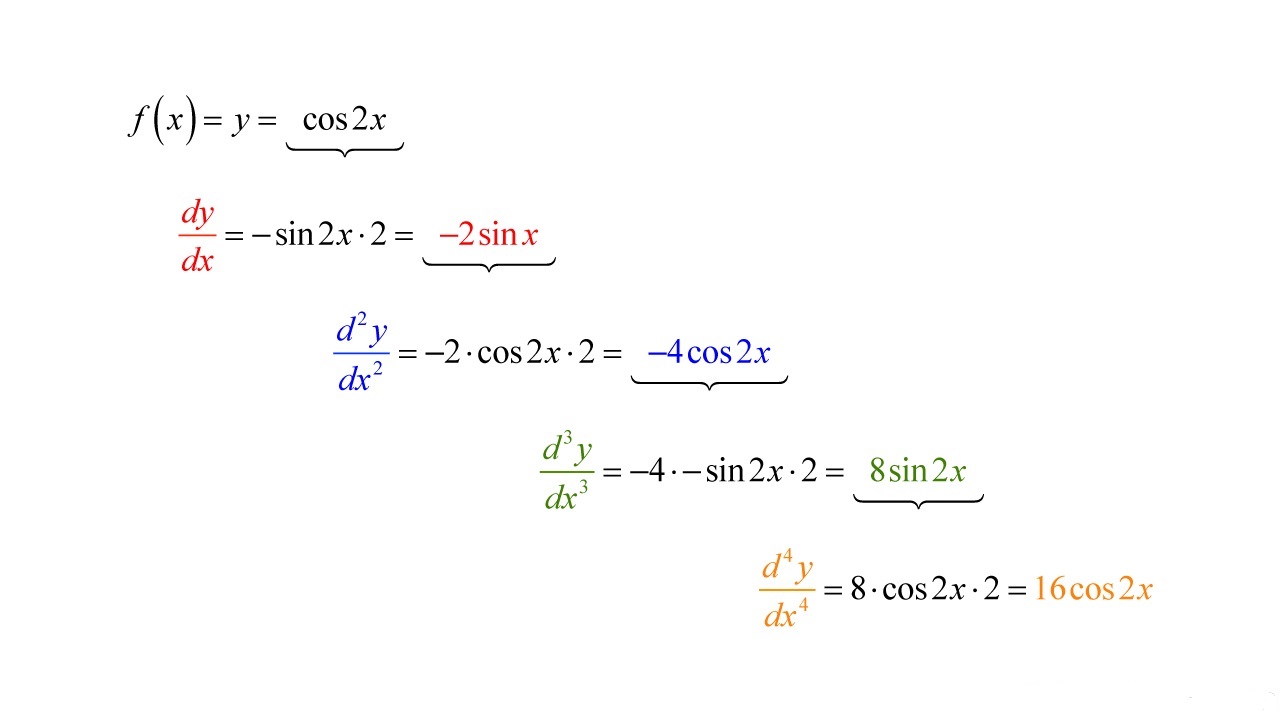
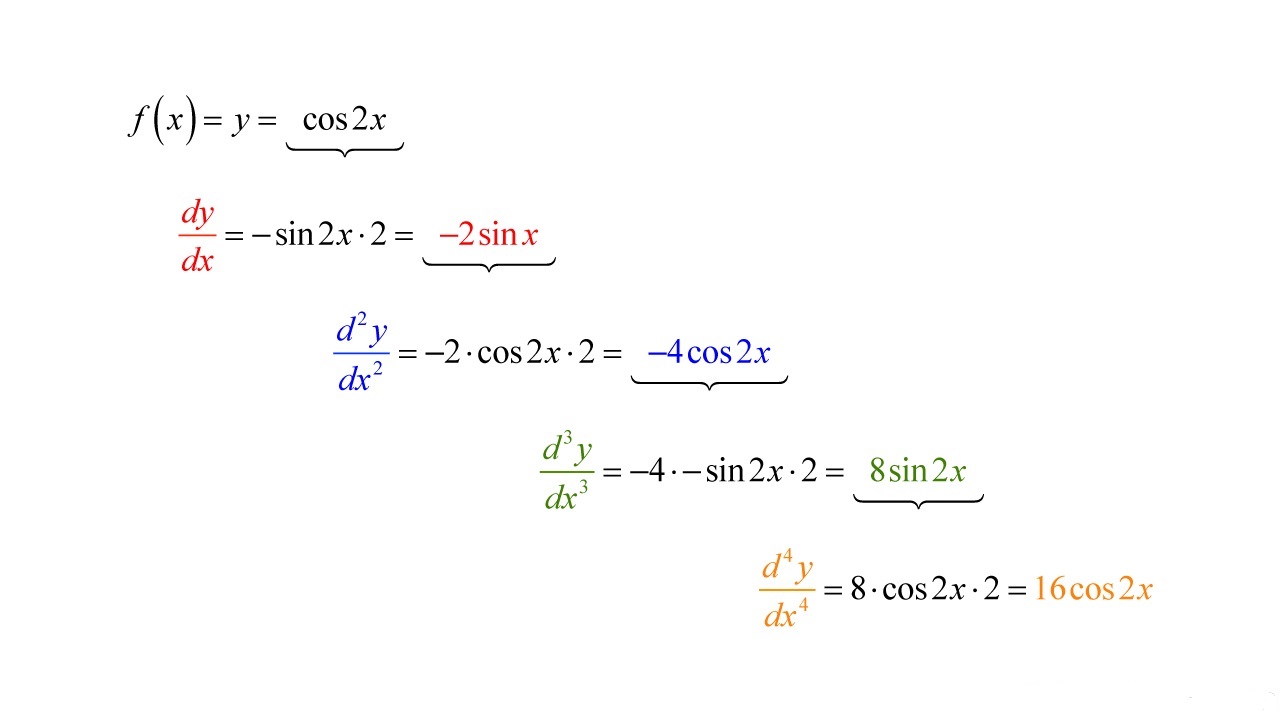
Finance
How To Find Higher Derivatives
Published: October 6, 2023
Learn how to find higher derivatives in finance and enhance your understanding of mathematical concepts for better financial analysis.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for LiveWell, at no extra cost. Learn more)
Table of Contents
Introduction
Derivatives play a crucial role in calculus and have a wide range of applications in various fields, including finance, physics, and engineering. They allow us to analyze the rate at which quantities change and provide valuable insights into the behavior of functions.
While most of us are familiar with the concept of derivatives, you may be wondering what exactly higher derivatives are. In calculus, higher derivatives refer to the derivatives of derivatives. They provide us with information about the rate of change of the rate of change, allowing for a deeper understanding of the underlying function.
In this article, we will explore how to find higher derivatives and understand their significance in calculus. We will discuss the process of calculating the second derivative and provide rules for finding higher order derivatives. Additionally, we will examine examples of finding higher derivatives and explore their practical applications in real-world scenarios.
Whether you are a student studying calculus or someone with a curiosity for mathematical concepts, understanding how to find higher derivatives will expand your knowledge and problem-solving abilities. So let’s dive in and unlock the power of higher derivatives!
Understanding Derivatives
Before we delve into higher derivatives, let’s first establish a solid understanding of derivatives themselves. In calculus, a derivative measures the rate at which a function changes at a particular point. It represents the slope of the tangent line to the function’s graph at that point. By calculating derivatives, we gain insights into how functions behave and can make predictions about their future behavior.
The derivative of a function f(x) is denoted by f'(x) or dy/dx. It represents the instantaneous rate of change of the function with respect to x. In simpler terms, it tells us how much the output of the function changes for a small change in the input.
Derivatives are fundamental in various areas, such as calculus, physics, and economics. They allow us to analyze motion, determine maximum and minimum points on a function, optimize processes, and more. For example, in physics, derivatives are used to calculate velocity and acceleration. In economics, they are used to analyze the demand and supply curves of goods.
The process of finding a derivative involves applying a set of rules and techniques. These include the power rule, product rule, quotient rule, and chain rule. These rules allow us to find the derivative of various types of functions, from polynomials to exponential and trigonometric functions.
To calculate the derivative of a function, we differentiate each term of the function separately and simplify the resulting expression. The derivative of a constant term is always zero, as it represents a horizontal line with no change.
It’s important to note that derivatives can have different meanings depending on the context. For example, in finance, derivatives refer to financial contracts whose value is based on an underlying asset. These derivatives are used for hedging against risks, speculating on price movements, and managing portfolios.
Now that we have a solid understanding of derivatives, let’s move on to higher derivatives and explore how they build upon this foundation.
What are Higher Derivatives?
In calculus, higher derivatives refer to the derivatives of derivatives. While the first derivative measures the rate of change of a function, higher derivatives provide information about the rate of change of the rate of change. This allows us to gain a deeper understanding of the behavior and characteristics of a function.
The n-th derivative of a function f(x) is denoted by f(n)(x) or dny/dxn. It represents the rate of change of the (n-1)-th derivative. In simpler terms, the second derivative measures how the first derivative changes, the third derivative measures how the second derivative changes, and so on.
When we talk about higher derivatives, we commonly refer to the second derivative, third derivative, and so on. These derivatives have distinct interpretations and applications in various fields.
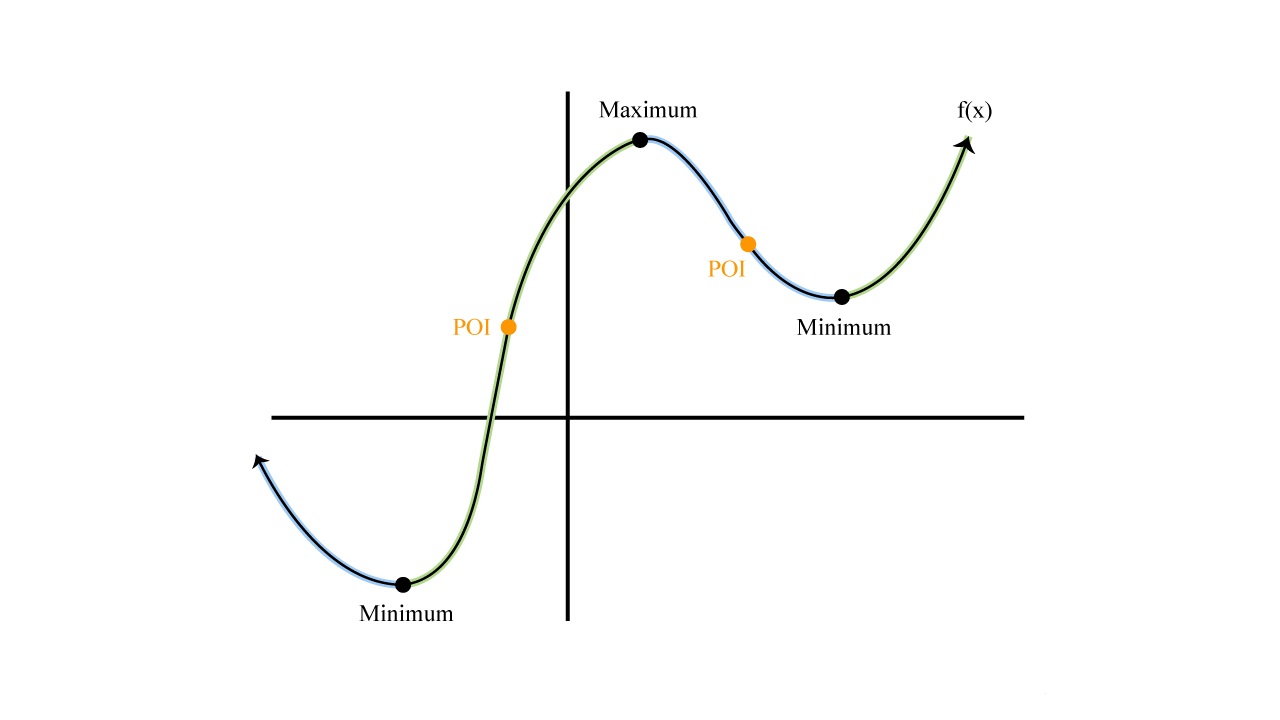
The second derivative, denoted as f”(x) or d2y/dx2, represents the rate of change of the slope of a function. It tells us whether the function is concave up (positive second derivative) or concave down (negative second derivative). Additionally, it helps identify points of inflection and plays a crucial role in optimization problems.
The third derivative, f”'(x) or d3y/dx3, represents the rate of change of the curvature of a function. It tells us how the curvature is changing at a given point on the function’s graph. The third derivative is useful in analyzing the behavior of functions and the shape of their graphs.
Higher derivatives beyond the third derivative have increasingly complex interpretations and are less commonly used. However, they can provide additional insights into the behavior of functions in specific scenarios.
Higher derivatives are particularly valuable in physics and engineering. They help analyze motion and acceleration, predict the behavior of systems, and solve differential equations. In finance, higher derivatives are used in options pricing models to estimate volatility and assess the sensitivity of option prices to changes in underlying variables.
Understanding higher derivatives allows us to delve deeper into the intricacies of functions and their behavior. By analyzing the rate of change of the rate of change, we can gain valuable insights and make more accurate predictions about various phenomena.
Calculating the Second Derivative
Calculating the second derivative of a function is a straightforward process that involves applying the rules of differentiation. The second derivative measures the rate of change of the slope of a function, providing insights into the curvature and concavity of the graph.
To find the second derivative, follow these steps:
- Differentiate the original function with respect to the variable x to find the first derivative.
- Take the derivative of the obtained first derivative to find the second derivative.
- Simplify the resulting expression if possible.
Let’s illustrate this process with an example. Consider the function f(x) = x^3 + 2x^2 + 3x. To find the second derivative, start by finding the first derivative of f(x).
Step 1: Find the first derivative:
f'(x) = 3x^2 + 4x + 3
Next, take the derivative of f'(x) to find the second derivative:
Step 2: Find the second derivative:
f”(x) = d/dx (f'(x))
f”(x) = d/dx (3x^2 + 4x + 3)
f”(x) = 6x + 4
So, the second derivative of f(x) = x^3 + 2x^2 + 3x is f”(x) = 6x + 4.
It’s worth noting that the second derivative represents the curvature of the function’s graph. If the second derivative is positive, the function is concave up, indicating a smile-like shape. If the second derivative is negative, the function is concave down, indicating a frown-like shape. Points where the second derivative changes from positive to negative or vice versa indicate inflection points.
Calculating the second derivative allows us to gain valuable insights into the behavior of functions. The curvature information it provides helps us analyze the shape of graphs, identify critical points, and make informed decisions in various mathematical and scientific fields.
Finding Higher Order Derivatives
Once we understand how to calculate the second derivative of a function, the process of finding higher order derivatives becomes relatively straightforward. To find the n-th derivative of a function, we follow a step-by-step approach that builds upon the rules of differentiation.
Here’s a general procedure for finding higher order derivatives:
- Find the first derivative of the function by differentiating it with respect to the variable.
- Repeat the differentiation process n times, where n represents the desired order of the derivative.
- Simplify the resulting expression.
Let’s illustrate this process with an example. Consider the function f(x) = e^x. We want to find the third derivative of this function.
Step 1: Find the first derivative:
f'(x) = d/dx (e^x) = e^x
Step 2: Find the second derivative:
f”(x) = d/dx (e^x) = e^x
Step 3: Find the third derivative:
f”'(x) = d/dx (e^x) = e^x
So, the third derivative of f(x) = e^x is f”'(x) = e^x.
It’s important to note that not all functions have finite higher order derivatives. Some functions may start repeating after a certain number of differentiations, indicating the end of the derivative process. In other cases, the derivative may diverge or become increasingly complex as the order increases.
Understanding how to find higher order derivatives enables us to analyze the behavior of functions in greater detail. By exploring successive rates of change, we gain deeper insights into the nature of functions, identifying patterns, critical points, and inflection points. Higher order derivatives find diverse applications in calculus, physics, engineering, and various scientific disciplines.
By applying the rules of differentiation and repeating the process, we can calculate any desired order of derivative for a given function. This empowers us to unravel the complexities of mathematical models and analyze the intricate relationships between variables.
Rules for Finding Higher Derivatives
When it comes to finding higher derivatives, a set of rules and formulas can simplify the process and make it more efficient. These rules build upon the fundamental rules of differentiation and provide a systematic approach to calculate higher order derivatives.
Here are some key rules for finding higher derivatives:
- Power Rule: The power rule allows us to differentiate terms with the form x^n, where n is a constant. For example, if f(x) = x^n, then the n-th derivative of f(x) can be found using the formula f(n)(x) = n(n-1)(n-2)…(n-(n-1))x^(n-n).
- Constant Rule: The derivative of a constant term, such as f(x) = c (where c is a constant), is always zero. This is because a constant term represents a horizontal line with no change.
- Sum/Difference Rule: The derivative of a sum or difference of two functions is equal to the sum or difference of their derivatives. For example, if f(x) = g(x) + h(x), then the n-th derivative of f(x) can be found by taking the n-th derivative of g(x) and h(x) separately and then adding or subtracting them.
- Product Rule: The product rule allows us to find the derivative of the product of two functions. If f(x) = g(x) * h(x), then the n-th derivative of f(x) can be determined using the formula f(n)(x) = ∑(k=0 to n) (nCk * g(k)(x) * h(n-k)(x)), where nCk represents the binomial coefficient.
- Quotient Rule: The quotient rule helps us find the derivative of the quotient of two functions. If f(x) = g(x) / h(x), then the n-th derivative of f(x) can be found using the formula f(n)(x) = (g(n)(x) * h(x) – g(x) * h(n)(x)) / (h(x))^((n+1)).
- Chain Rule: The chain rule is applied when differentiating composite functions. If f(x) = g(h(x)), where g(x) and h(x) are functions, then the n-th derivative of f(x) can be calculated by multiplying the n-th derivative of g(h(x)) with the n-th derivative of h(x).
By utilizing these rules, we can simplify the process of finding higher derivatives and avoid repetitive calculations. These rules serve as powerful tools in calculus and enable us to analyze complex functions and systems more efficiently.
It’s important to note that based on the complexity of the function and the desired order of the derivative, it may be necessary to apply multiple rules in combination to calculate the higher derivative accurately. Practice and familiarity with these rules will make the process more intuitive and allow for quicker evaluation of higher derivatives.
Examples of Finding Higher Derivatives
Let’s explore some examples to illustrate how to find higher derivatives using the rules and techniques we discussed earlier. These examples will demonstrate the step-by-step process of calculating higher order derivatives and provide a solid understanding of their application.
Example 1: Find the fourth derivative of the function f(x) = 3x^4 – 2x^3 + 5x^2 – 7x + 2.
Solution:
To find the fourth derivative, we need to differentiate the function four times. Let’s begin:
- First derivative:
- f'(x) = d/dx (3x^4 – 2x^3 + 5x^2 – 7x + 2)
- f'(x) = 12x^3 – 6x^2 + 10x – 7
- Second derivative:
- f”(x) = d/dx (12x^3 – 6x^2 + 10x – 7)
- f”(x) = 36x^2 – 12x + 10
- Third derivative:
- f”'(x) = d/dx (36x^2 – 12x + 10)
- f”'(x) = 72x – 12
- Fourth derivative:
- f””(x) = d/dx (72x – 12)
- f””(x) = 72
Therefore, the fourth derivative of f(x) = 3x^4 – 2x^3 + 5x^2 – 7x + 2 is f””(x) = 72.
Example 2: Find the third derivative of the function f(x) = sin(2x).
Solution:
To find the third derivative, we differentiate the function three times. Let’s proceed:
- First derivative:
- f'(x) = d/dx (sin(2x))
- f'(x) = 2cos(2x)
- Second derivative:
- f”(x) = d/dx (2cos(2x))
- f”(x) = -4sin(2x)
- Third derivative:
- f”'(x) = d/dx (-4sin(2x))
- f”'(x) = -8cos(2x)
Therefore, the third derivative of f(x) = sin(2x) is f”'(x) = -8cos(2x).
These examples demonstrate the process of finding higher derivatives using the rules of differentiation. By applying these rules and techniques, we can determine the rate of change of the rate of change and gain insights into the behavior of functions at various levels.
Applications of Higher Derivatives
Higher derivatives have diverse applications in various fields, ranging from mathematics and physics to economics and engineering. They provide valuable insights into the behavior, characteristics, and relationships of functions, allowing for precise analysis and prediction.
Here are some common applications of higher derivatives:
- Curve Sketching: Higher derivatives play a crucial role in curve sketching. By analyzing the concavity and inflection points of a function using the second derivative, we can create accurate and detailed graphs, visualizing its behavior and characteristics.
- Optimization: Higher derivatives aid in optimization problems. To find maximum or minimum values of a function, we can use the second derivative test, which examines the concavity and critical points. This is especially useful in areas like economics, where optimization is essential for maximizing profit or minimizing cost.
- Physics and Mechanics: Higher derivatives have significant applications in physics and mechanics. They help analyze motion, acceleration, and the behavior of physical systems. By calculating higher derivatives, we can determine the rate of change of acceleration, jerk (rate of change of acceleration), snap (rate of change of jerk), and other important quantities used in the study of kinetics and dynamics.
- Control Systems Engineering: Higher derivatives are employed in control systems engineering to design and analyze the behavior of systems. By studying higher derivatives of system responses, engineers can evaluate stability and responsiveness, improve performance, and ensure accurate control of various processes, such as robotics, manufacturing, and automation.
- Financial Derivatives: In the field of finance, the term “derivatives” refers to financial contracts whose value is derived from an underlying asset. Higher derivatives, such as gamma and vega, are used in options pricing models to estimate volatility and assess the sensitivity of option prices to changes in the underlying stock price or other variables. These derivatives help investors manage risks and make informed investment decisions.
These applications represent just a fraction of the wide range of uses for higher derivatives. They are essential tools in advanced mathematical modeling, scientific research, and real-world problem-solving. By leveraging the insights provided by higher derivatives, we can make more accurate predictions, optimize systems, and gain a deeper understanding of the complex dynamics at play in various disciplines.
Conclusion
Higher derivatives are powerful tools in calculus that allow us to explore the rate of change of the rate of change of a function. By calculating higher order derivatives, we gain insights into the behavior, shape, and characteristics of functions, providing valuable information for analysis and prediction.
In this article, we have covered the fundamental concepts of derivatives, understanding how they measure the rate of change of a function. We then delved into higher derivatives, discovering their importance in analyzing the rate of change of the rate of change.
We explored the process of calculating the second derivative and discussed the rules and techniques for finding higher order derivatives. These rules, including the power rule, sum/difference rule, product rule, quotient rule, and chain rule, simplify the process and enable us to calculate higher derivatives efficiently.
Through examples, we illustrated how to find higher derivatives, applying the rules and formulas. These examples showcased how higher derivatives can be calculated step by step, providing clear demonstrations of their applications.
Moreover, we explored the practical applications of higher derivatives in fields such as curve sketching, optimization, physics, control systems engineering, and finance. These applications highlight the diverse use cases and the impact of higher derivatives beyond theoretical calculus.
In conclusion, understanding how to find higher derivatives expands our knowledge of calculus and enhances our problem-solving skills. It equips us with powerful tools to analyze functions, optimize systems, predict behavior, and make informed decisions across various disciplines. Embracing the power of higher derivatives opens up a world of possibilities and deepens our understanding of the intricate relationships at play in the mathematical and scientific realms.