What Is Number Bonds

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for LiveWell, at no extra cost. Learn more)

Introduction

Number bonds are an essential concept in mathematics that play a crucial role in understanding the fundamental relationship between numbers. They provide a strong foundation for mathematical operations and problem-solving skills. Number bonds help students develop a deeper understanding of addition, subtraction, multiplication, and division by breaking down numbers into smaller parts.

In simple terms, number bonds depict the relationship between a whole number and its parts. By exploring number bonds, students can comprehend how numbers are composed and decomposed, leading to a greater grasp of mathematical concepts. This concept is particularly crucial in early childhood education as it sets the stage for more complex mathematical ideas in later years.

The purpose of number bonds is to strengthen a student’s number sense and build a solid mathematical foundation. It helps students visualize the connection between numbers and enables them to manipulate and explore different number combinations. Number bonds provide a structured approach to learning and offer a systematic way to understand the basic principles of arithmetic. Moreover, number bonds facilitate mental calculations, making it easier for students to perform calculations mentally.

Understanding number bonds is beneficial for students in numerous ways. Firstly, it enhances their problem-solving skills by enabling them to break down complex problems into simpler parts. By grasping the concept of number bonds, students can approach mathematical challenges with confidence and find innovative solutions. Additionally, number bonds foster critical thinking skills as students analyze and evaluate different number combinations.

Furthermore, number bonds pave the way for better mathematical fluency. By internalizing number relationships, students can swiftly recall number facts and perform calculations efficiently. This fluency is crucial for tackling more advanced mathematical concepts in higher grades.

Definition of Number Bonds

Number bonds can be defined as the concept of breaking down a number into its component parts or combining multiple numbers to form a whole. It is a way of understanding the relationship between numbers and how they can be combined or separated.

In a number bond, there are three components: the whole, the parts, and the bond. The whole represents the total number, while the parts are the individual numbers that make up the whole. The bond is the connection or relationship between the whole and the parts.

For example, let’s take the number 10. In a number bond for 10, it can be broken down into different parts, such as 6 and 4 or 7 and 3. The bond between the parts and the whole shows that when the parts are combined, they make up the whole number.

Number bonds are often represented visually using circles or squares. The whole number is typically placed in the center, and the parts are placed in the outer circles or squares, with lines drawn to show the connection or bond between them.

Number bonds are not limited to addition and can also be applied to subtraction, multiplication, and division. In subtraction, number bonds help students understand how a larger number can be broken down into smaller parts. For example, the number bond for 8 in subtraction could be represented as 10 (whole) – 2 (part) = 8.

In multiplication, number bonds illustrate how factors can be combined to form a product. For example, the number bond for 12 in multiplication could be represented as 3 (part) x 4 (part) = 12 (whole).

In division, number bonds demonstrate how a dividend can be divided into equal parts. For example, the number bond for 15 in division could be represented as 30 (dividend) ÷ 2 (part) = 15 (whole).

Overall, number bonds provide a conceptual framework for understanding the relationships between numbers and are a valuable tool for building a solid foundation in mathematics.

Purpose of Number Bonds

The purpose of number bonds is to develop a strong number sense and mathematical foundation by helping students understand the relationship between numbers. Number bonds serve as a fundamental building block for addition, subtraction, multiplication, and division skills. They provide a visual and conceptual representation of how numbers can be composed or decomposed, enabling students to grasp mathematical concepts more effectively.

One of the main purposes of number bonds is to enhance a student’s ability to perform mental calculations. By understanding number bonds, students can break down numbers into smaller, more manageable parts, making mental arithmetic easier. For example, when adding 9 + 3, a student familiar with number bonds can recognize that 9 can be decomposed into 6 and 3, resulting in a mental calculation of 6 + 3 = 9 + 3 = 12. This fluency in mental calculations improves overall mathematical efficiency.

Number bonds also facilitate the development of problem-solving skills. By breaking down numbers into their component parts, students can analyze and solve mathematical problems more effectively. For example, when faced with a word problem that requires finding a missing number in an equation, understanding number bonds allows students to identify the missing part or whole and solve the problem systematically.

Furthermore, number bonds promote critical thinking and mathematical reasoning. By exploring different number combinations and relationships, students develop a deeper understanding of the properties of numbers. They learn to analyze number patterns, identify number relationships, and make connections between different mathematical concepts.

Additionally, number bonds provide students with a solid foundation for more advanced mathematical concepts. Once students have a firm grasp of number bonds, they can apply this knowledge to more complex operations such as multi-digit addition, subtraction, multiplication, and division. Number bonds become a mental tool that students can use to break down and manipulate larger numbers, leading to a deeper understanding of mathematical operations.

Ultimately, the purpose of number bonds is to empower students with a strong number sense, mental computational skills, and problem-solving abilities. By understanding the relationship between numbers through number bonds, students not only develop their mathematical abilities but also build confidence and enjoyment in mathematics.

Benefits of Number Bonds

The use of number bonds in mathematics offers numerous benefits for students at various educational levels. These benefits go beyond computational skills and contribute to their overall mathematical understanding and problem-solving abilities. Here are some key benefits of incorporating number bonds into the learning process:

1. Conceptual Understanding: Number bonds help students develop a deeper conceptual understanding of numbers and operations. By breaking down numbers into their component parts, students can see the relationship and connection between different numbers, fostering a solid foundation for further mathematical learning.

2. Mental Computation: Understanding number bonds enhances mental computation skills. Students can quickly recognize compatible number combinations and mentally calculate arithmetic problems by leveraging their knowledge of number bonds. This fluency in mental computation saves time and builds computational efficiency.

3. Problem-Solving Skills: Number bonds support problem-solving skills by enabling students to break down complex problems into smaller, more manageable parts. By identifying number bonds within a problem, students can solve equations systematically and apply this problem-solving approach to a wide range of mathematical scenarios.

4. Flexible Thinking: Working with number bonds encourages flexible thinking and multiple strategies for solving mathematical problems. Students can explore different combinations and decompositions of numbers, fostering a growth mindset and promoting creative problem-solving strategies.

5. Mathematical Fluency: Through consistent practice with number bonds, students develop mathematical fluency. They gain confidence in recognizing and recalling number combinations, which helps them solve problems more efficiently and accurately.

6. Number Sense Development: Number bonds contribute to the development of number sense, which is essential for mathematical proficiency. By working with number bonds, students develop an intuitive sense of numbers, understanding their magnitude, relationships, and properties.

7. Enthusiasm for Mathematics: Incorporating number bonds into the classroom can foster enthusiasm for mathematics. The visual and interactive nature of number bonds engages students, making mathematical concepts more accessible and enjoyable.

8. Real-World Application: Number bonds have real-world applications, helping students understand how mathematics is relevant and applicable in everyday life. By recognizing number relationships, students can make connections to real-world scenarios, such as dividing a set of objects into equal groups or calculating a discount during a sale.

In summary, incorporating number bonds into mathematics education provides a range of benefits. From developing conceptual understanding and mental computation skills to promoting problem-solving abilities and fostering a love for mathematics, number bonds empower students with a solid mathematical foundation and the skills necessary for future mathematical success.

Number Bonds Techniques

There are several techniques and strategies that can be used to teach and reinforce number bonds in the classroom. These techniques help students develop a solid understanding of number relationships and enhance their computational skills. Here are some effective number bonds techniques:

1. Manipulatives: Hands-on manipulatives, such as counters, cubes, or linking blocks, provide a tangible and visual representation of number bonds. Students can physically manipulate the manipulatives to create different number combinations, reinforcing the concept of number relationships.

2. Visual Representations: Using visual representations, such as circles or squares, can help students visualize the number bonds. Placing the whole number in the center and the parts in surrounding circles/squares with connecting lines reinforces the bond between the numbers.

3. Number Bond Mats: Number bond mats are specific worksheet templates designed for students to fill in the missing parts or wholes. These mats provide a structured format for practicing number bonds and can be customized for different numbers and operations.

4. Number Bonds Games: Incorporating games into the learning process adds an element of fun and engagement. Number bond games can involve matching number cards, dice games, or board games that require students to identify number combinations and make connections between numbers.

5. Number Bond Puzzles: Number bond puzzles provide a problem-solving approach to practice number bonds. Students are given a partially completed number bond, and they have to determine the missing part or whole to complete the puzzle, requiring critical thinking and logical reasoning.

6. Fact Families: Fact families are a related concept to number bonds and help reinforce the connection between addition and subtraction. Teaching students that addition and subtraction facts are related can enhance their understanding of number relationships and the concept of number bonds.

7. Number Bond Flip Charts: Flip charts with flippable cards allow students to manipulate the numbers and explore different number combinations. Students can flip the cards to create new number bonds and visualize the relationships between the whole and the parts.

8. Technology Tools: Technology tools, such as interactive whiteboards or educational apps, can provide virtual manipulatives and interactive activities to practice number bonds. These tools offer engaging and interactive experiences that support students’ understanding and fluency with number bonds.

It’s important to remember that different students may respond better to different techniques. Teachers should use a combination of these strategies to cater to individual learning styles and provide a variety of opportunities for students to practice and reinforce their understanding of number bonds.

Examples of Number Bonds

Number bonds can be seen in various mathematical scenarios, and understanding these examples helps students grasp the concept of number bonds more effectively. Here are a few examples:

Example 1: Addition: Consider the number bond for 8: 3 + 5 = 8. In this example, 8 is the whole number, and 3 and 5 are the parts. The number bond shows that when the parts 3 and 5 are added together, they form the whole number 8.

Example 2: Subtraction: For the number bond related to subtraction, let’s take 10 as the whole number: 10 – 3 = 7. In this case, 10 is the whole number, 3 is one part, and 7 is the other part. The number bond illustrates that when the part 3 is subtracted from the whole 10, it gives the remaining part 7.

Example 3: Multiplication: Looking at the number bond for multiplication, consider the number 12: 4 x 3 = 12. Here, 12 is the whole number, 4 is one part, and 3 is the other part. The number bond demonstrates that when the part 4 is multiplied by the part 3, it results in the whole number 12.

Example 4: Division: Let’s explore the number bond for division, with 20 as the whole number: 20 ÷ 4 = 5. In this case, 20 is the dividend, 4 is one part, and 5 is the other part. The number bond reveals that when the dividend 20 is divided by the part 4, it yields the whole number 5.

Example 5: Fact Families: Fact families are related number bonds that involve both addition and subtraction. Take the fact family for 8: 3 + 5 = 8 and 8 – 5 = 3. In this example, the number bond shows that 8 can be broken down into the parts 3 and 5 in an addition equation, and the subtraction equation demonstrates that when the part 5 is subtracted from the whole 8, the remaining part is 3.

These examples illustrate how number bonds depict the relationship between numbers in different mathematical operations. By understanding and recognizing number bonds in various contexts, students can develop a solid foundation for mathematical fluency and problem-solving skills.

Application of Number Bonds in Mathematics

Number bonds have numerous applications in mathematics across various topics and concepts. By understanding and utilizing number bonds, students can enhance their problem-solving abilities, computational skills, and overall mathematical understanding. Here are some key areas where number bonds find practical application:

1. Mental Math: Number bonds are instrumental in mental calculations. By breaking down numbers into their component parts, students can perform mental addition, subtraction, multiplication, and division more efficiently. For example, when mentally calculating 9 + 6, a student familiar with number bonds can recognize that 9 can be split as 5 + 4, making the calculation easier as 5 + 4 + 6 = 15.

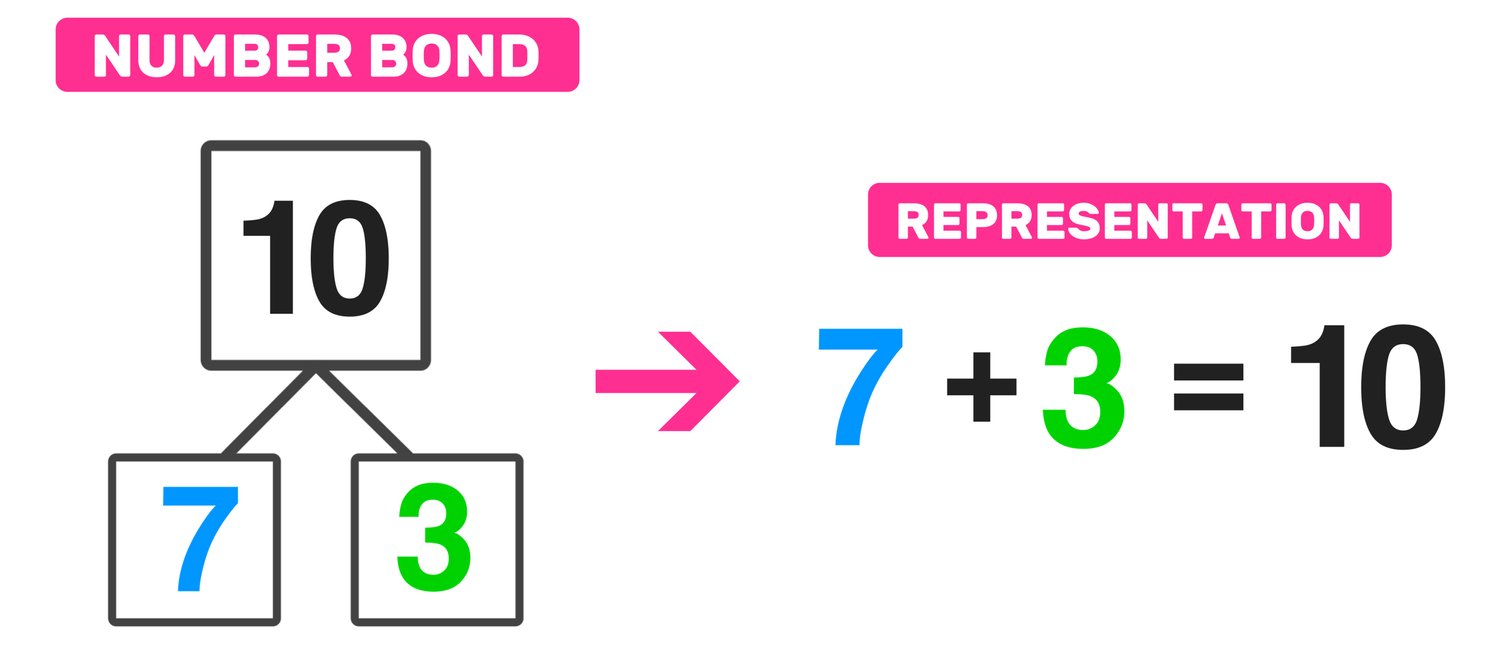
2. Fact Fluency: Number bonds contribute to the development of fact fluency. By recognizing number bonds and the connection between numbers, students can quickly recall addition and subtraction facts. For example, when faced with the question 7 + 3, a student familiar with number bonds will immediately recognize that the answer is 10, based on the number bond for 10 = 7 + 3.

3. Understanding Place Value: Number bonds help students understand the concept of place value. By breaking down numbers into their component parts, students can see the relationship between tens and ones. For example, in the number bond for 34, students recognize that 30 is made up of 3 tens and 4 is made up of 4 ones.

4. Fraction Relationships: Number bonds can be used to teach fraction relationships. By using number bonds, students can visually represent fractions as parts of a whole. For example, in the number bond for 1, students can see that 1 can be represented as 1/2 + 1/2 or 1/3 + 2/3, helping them grasp the concept of equivalent fractions.

5. Multiplication and Division Strategies: When learning multiplication and division, number bonds can be used to illustrate fact families and the relationship between numbers. By recognizing number bonds, students can apply strategies such as skip counting or splitting numbers to simplify calculations. For example, when solving 6 x 8, students can notice the number bond 6 + 2 = 8, and use that to mentally calculate the answer as 48.

6. Problem-Solving: Number bonds aid students in solving mathematical problems. By breaking down numbers and recognizing relationships, students can approach complex problems with a structured and systematic mindset. Number bonds help students analyze and solve problems more effectively, and make connections between different mathematical concepts.

These applications of number bonds in mathematics highlight the versatility and importance of understanding number relationships and composition. By incorporating number bonds into mathematical learning, students gain a stronger grasp of mathematical concepts, develop problem-solving skills, and build a solid foundation for future mathematical success.

Number Bonds in Early Childhood Education

Number bonds play a vital role in early childhood education as they form the building blocks for mathematical understanding and lay the foundation for future mathematical skills. Introducing number bonds in early childhood education helps young learners develop a strong number sense, computational fluency, and problem-solving abilities. Here are some key reasons why number bonds are essential in early childhood education:

1. Conceptual Understanding: Number bonds provide young children with a concrete and visual representation of numbers and their relationships. By using manipulatives and visual aids, children can physically see and touch the parts that make up a whole. This hands-on approach fosters a deep conceptual understanding of numbers, paving the way for more complex mathematical concepts later on.

2. Counting and Cardinality: Number bonds help children develop the foundational skills of counting and cardinality. By understanding how numbers can be composed and decomposed, children learn to count in a structured, organized manner. For example, they will understand that 5 is made up of 2 and 3, and that when counting forwards or backwards, they can break larger numbers into smaller, more manageable parts.

3. Mental Math Strategies: Introducing number bonds at an early age helps children develop mental math strategies. They learn to recognize number combinations and use them to solve problems mentally. For instance, when faced with the equation 8 + 4, children familiar with number bonds will quickly recognize that 8 and 4 make 12 without having to count on their fingers.

4. Problem-Solving Skills: Number bonds support the development of problem-solving skills. By breaking down numbers and understanding their relationships, children gain the ability to approach and solve mathematical problems systematically. Number bonds provide a problem-solving framework that encourages critical thinking and logical reasoning.

5. Mathematical Fluency: Early exposure to number bonds helps children develop mathematical fluency. By recognizing and understanding number bonds, children can quickly recall number combinations and perform calculations efficiently. This fluency lays the groundwork for future mathematical success.

6. Building Confidence: Introducing number bonds in early childhood education boosts children’s confidence in their mathematical abilities. As they gain a strong understanding of number relationships, children feel more confident in tackling math problems and are more willing to explore and engage with the subject.

7. Preparation for Higher-Level Mathematics: Number bonds serve as the stepping stones for more advanced mathematical concepts. When children have a solid foundation in understanding number relationships, they can easily grasp more complex topics like place value, operations with larger numbers, and algebraic thinking in their later educational journey.

Incorporating number bonds into early childhood education provides children with a strong foundation in mathematics. By focusing on understanding the relationships between numbers, children develop not only mathematical skills but also critical thinking, problem-solving abilities, and mathematical confidence, setting them on a path towards mathematical success in the future.

Conclusion

Number bonds are a critical concept in mathematics that lays the groundwork for a strong mathematical foundation. By understanding the relationship between a whole number and its parts, students develop essential skills in addition, subtraction, multiplication, and division. Number bonds enable students to visualize and manipulate numbers, enhancing mental computation and problem-solving abilities. Moreover, number bonds promote a conceptual understanding of numbers, building number sense and mathematical fluency.

The purpose of number bonds is to provide students with a structured approach to learning, enabling them to break down complex problems into simpler parts. This approach enhances their problem-solving skills and fosters critical thinking and flexible mathematical reasoning. Number bonds also play a vital role in early childhood education, as they help young learners develop a strong number sense, computational fluency, and a solid understanding of mathematical relationships.

The benefits of number bonds extend beyond mathematics. The ability to mentally calculate, apply strategies, and problem-solve using number bonds prepares students for success in the real world, where numeracy skills are essential in everyday situations.

In conclusion, number bonds are an integral part of mathematics education, offering a structured and systematic approach to understanding number relationships. By incorporating number bonds into the curriculum, educators empower students with the tools they need to excel in mathematics, cultivate critical thinking skills, and lay a strong foundation for future mathematical success.