How To Find If A Function Is Increasing Or Decreasing Using Derivatives

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for LiveWell, at no extra cost. Learn more)

Introduction

In the field of mathematics, understanding the behavior of functions is crucial in various applications, including finance. One fundamental concept related to function behavior is whether a function is increasing or decreasing.

Knowing whether a function is increasing or decreasing is valuable because it provides insights into how the function behaves as its input values change. Specifically, an increasing function indicates that as the input increases, the output also increases. On the other hand, a decreasing function suggests that as the input increases, the output decreases.

This knowledge is especially useful in finance, where the analysis of market trends and investment performance often relies on understanding the direction of change.

In this article, we will explore the methods for identifying if a function is increasing or decreasing using derivatives. Derivatives are a powerful tool in calculus that allows us to study the rate of change of a function at any given point.

We will cover two main tests: the first derivative test and the second derivative test. These tests involve analyzing the sign of the derivatives to determine the behavior of the function.

By mastering these tests, you will be equipped with the skills to analyze and understand the behavior of functions in various financial scenarios. Let’s dive in!

Definition of increasing and decreasing functions

Before we delve into the methods for determining if a function is increasing or decreasing, let’s start by defining what exactly these terms mean in the context of functions.

An increasing function is one where the output (or the value of the function) increases as the input (or the independent variable) increases. In other words, as we move from left to right along the x-axis, the y-values of an increasing function go up.

On the other hand, a decreasing function is one where the output decreases as the input increases. In this case, as we move along the x-axis from left to right, the y-values of a decreasing function go down.

To illustrate this concept, consider the graph of a simple linear function: f(x) = 2x. As we increase the value of x, the output (y-value) increases in a linear fashion. Therefore, the function f(x) = 2x is an increasing function.

Conversely, imagine a quadratic function with the equation f(x) = -x^2. As we increase the value of x, the output (y-value) decreases. Consequently, the function f(x) = -x^2 is a decreasing function.

It’s important to note that a function can be increasing or decreasing over certain intervals while exhibiting the opposite behavior in other intervals. Additionally, some functions may neither be strictly increasing nor strictly decreasing, but instead exhibit a constant behavior over certain intervals.

Now that we have a clear understanding of what it means for a function to be increasing or decreasing, we can move on to learning the tests and techniques for determining these characteristics using derivatives.

First Derivative Test

The first derivative test is a powerful tool for determining if a function is increasing or decreasing. It involves analyzing the sign of the first derivative of the function at specific points.

To apply the first derivative test, we need to start by finding the derivative of the function. The derivative represents the rate of change of the function at any given point.

Here’s how the first derivative test works:

1. Find the first derivative of the function.
2. Solve for the critical points of the function by setting the first derivative equal to zero and solving for the x-values.
3. Plot the critical points on a number line.
4. Choose test points within each interval formed by the critical points and evaluate the sign of the derivative at those points.
5. Determine the behavior of the function based on the signs of the derivative in each interval:
• If the derivative is positive, the function is increasing in that interval.
• If the derivative is negative, the function is decreasing in that interval.

By analyzing the sign of the derivative, we can identify the intervals where the function is increasing or decreasing. This information provides valuable insights into the behavior of the function.

It’s important to note that the first derivative test assumes the differentiability of the function, meaning that the derivative exists for all points in the domain of the function. It is also worth mentioning that the test can only determine if the function is strictly increasing or decreasing. To determine if the function is non-decreasing or non-increasing (allowing for constant intervals), further analysis is required.

Now that we understand the first derivative test, let’s practice applying it with some example problems to solidify our understanding.

Steps to Determine if a Function is Increasing or Decreasing using the First Derivative

Now that we are familiar with the first derivative test, let’s dive into the step-by-step process for using the first derivative to determine if a function is increasing or decreasing:

1. Start by finding the first derivative of the function.
2. Simplify the derived expression as much as possible.
3. Solve the derived expression for values of x that make the derivative equal to zero. These points are known as critical points.
4. Plot the critical points on a number line.
5. Select test points within each interval created by the critical points. These test points will help us determine the sign of the derivative in each interval.
6. Evaluate the derived expression at each test point to determine whether it is positive or negative.
7. Analyze the signs of the derivative in each interval:
• If the derivative is positive, the function is increasing in that interval.
• If the derivative is negative, the function is decreasing in that interval.
• If the derivative is zero, the function may have a relative maximum or minimum at that point.

By following these steps, we can systematically determine the intervals where the function is increasing or decreasing. This information is valuable in understanding the behavior of the function and can be applied in various financial scenarios to analyze trends and make informed decisions.

Remember, the first derivative test assumes the differentiability of the function and can only determine if the function is strictly increasing or decreasing. For non-strictly increasing or decreasing functions, additional analysis is required.

Now that we have a clear understanding of the steps involved, let’s put our knowledge into practice with some example problems.

Example Problems

Now, let’s work through a couple of example problems to solidify our understanding of how to determine if a function is increasing or decreasing using the first derivative and the first derivative test.

Example 1:

Consider the function f(x) = 3x^2 – 6x + 2. We will use the first derivative test to determine if the function is increasing or decreasing.

1. Find the first derivative of the function: f'(x) = 6x – 6.
2. Simplify the derived expression: f'(x) = 6(x – 1).
3. Solve the derived expression for x: 6(x – 1) = 0 ⟶ x = 1.
4. Plot the critical point x = 1 on a number line.
5. Select test points within each interval: x = 0 and x = 2.
6. Evaluate the derivative at the test points: f'(0) = 6(0 – 1) = -6 and f'(2) = 6(2 – 1) = 6.
7. Analyze the signs of the derivative in each interval:
   • For x < 1, f'(x) = -6, indicating that the function is decreasing in this interval.
   • For x > 1, f'(x) = 6, indicating that the function is increasing in this interval.

Therefore, we conclude that the function f(x) = 3x^2 – 6x + 2 is decreasing for x < 1 and increasing for x > 1.

Example 2:

Let’s consider the function g(x) = -2x^3 + 9x^2 – 12x + 4 and determine if it is increasing or decreasing using the first derivative test.

1. Find the first derivative of the function: g'(x) = -6x^2 + 18x – 12.
2. Simplify the derived expression: g'(x) = 6(3 – x).
3. Solve the derived expression for x: 6(3 – x) = 0 ⟶ x = 3.
4. Plot the critical point x = 3 on a number line.
5. Select test points within each interval: x = 2 and x = 4.
6. Evaluate the derivative at the test points: g'(2) = 6(3 – 2) = 6 and g'(4) = 6(3 – 4) = -6.
7. Analyze the signs of the derivative in each interval:
   • For x < 3, g'(x) = 6, indicating that the function is increasing in this interval.
   • For x > 3, g'(x) = -6, indicating that the function is decreasing in this interval.

Therefore, we conclude that the function g(x) = -2x^3 + 9x^2 – 12x + 4 is increasing for x < 3 and decreasing for x > 3.

By working through these example problems, we gain practical experience in applying the first derivative test to determine if a function is increasing or decreasing. Remember to verify your answers with additional tests and analysis if needed.

Second Derivative Test

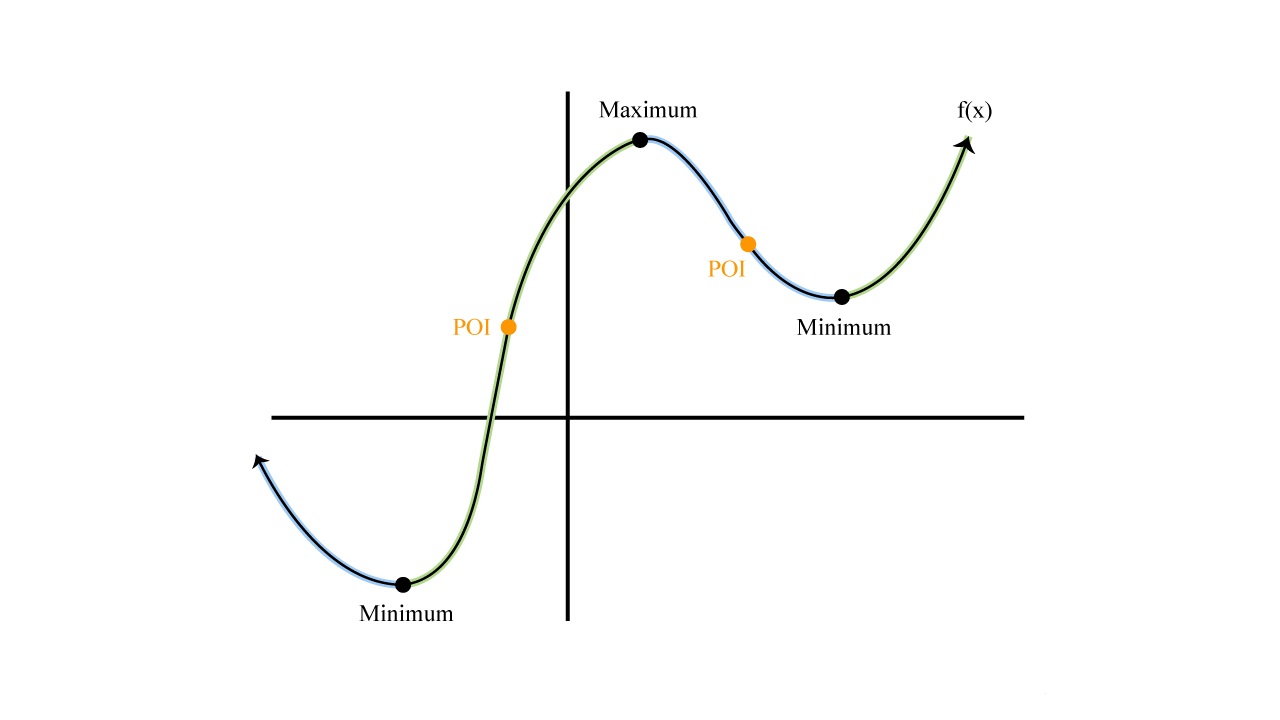
In addition to the first derivative test, another method for determining if a function is increasing or decreasing is by using the second derivative. The second derivative provides information about the concavity of a function.

The concavity of a function refers to its curvature or the direction in which it curves. A function can either be concave up, meaning it curves like a smiley face, or concave down, meaning it curves like a frown.

The second derivative test allows us to determine if a function is increasing or decreasing based on the concavity of the function at specific points.

Here’s how the second derivative test works:

1. Find the second derivative of the function.
2. Simplify the derived expression as much as possible.
3. Solve for the critical points of the function by setting the first derivative equal to zero and solving for the x-values.
4. Plot the critical points on a number line.
5. Choose test points within each interval formed by the critical points and evaluate the sign of the second derivative at those points.
6. Determine the behavior of the function based on the signs of the second derivative in each interval:
• If the second derivative is positive, the function is concave up and increasing in that interval.
• If the second derivative is negative, the function is concave down and decreasing in that interval.

The second derivative test provides additional insights into the behavior of a function by considering not only the signs of the derivative but also the concavity of the function.

Let’s continue our exploration of function behavior by learning the steps to determine if a function is increasing or decreasing using the second derivative.

Steps to Determine if a Function is Increasing or Decreasing using the Second Derivative

Now that we understand the second derivative test, let’s walk through the step-by-step process for determining if a function is increasing or decreasing using the second derivative:

1. Start by finding the second derivative of the function.
2. Simplify the derived expression as much as possible.
3. Solve the derived expression for values of x that make the second derivative equal to zero. These points are known as inflection points.
4. Plot the inflection points on a number line.
5. Select test points within each interval created by the inflection points. These test points will help us determine the sign of the second derivative in each interval.
6. Evaluate the derived expression of the second derivative at each test point to determine whether it is positive or negative.
7. Analyze the signs of the second derivative in each interval:
   • If the second derivative is positive, the function is concave up and increasing in that interval.
   • If the second derivative is negative, the function is concave down and decreasing in that interval.
   • If the second derivative changes sign at an inflection point, it indicates a change in concavity.

By following these steps, we can determine the intervals where a function is increasing or decreasing based on the concavity of the function. This additional information about the curvature of the function enhances our understanding of its behavior.

It’s important to note that the second derivative test assumes that the function is twice differentiable, meaning both the first and second derivatives exist for all points in the domain of the function. Additionally, if the second derivative is zero at a specific point, further analysis is required to determine the nature of that point.

Now that we are familiar with the steps involved, let’s put our knowledge into practice with some example problems.

Example Problems

Now, let’s apply the second derivative test to some example problems in order to further solidify our understanding of how to determine if a function is increasing or decreasing based on the concavity of the function using the second derivative.

Example 1:

Consider the function f(x) = x^3 – 3x^2 + 2x. We will use the second derivative test to determine if the function is increasing or decreasing.

1. Find the second derivative of the function: f”(x) = 6x – 6.
2. Simplify the derived expression: f”(x) = 6(x – 1).
3. Solve the derived expression for x: 6(x – 1) = 0 ⟶ x = 1.
4. Plot the inflection point x = 1 on a number line.
5. Select test points within each interval: x = 0 and x = 2.
6. Evaluate the second derivative at the test points: f”(0) = 6(0 – 1) = -6 and f”(2) = 6(2 – 1) = 6.
7. Analyze the signs of the second derivative in each interval:
   • For x < 1, f''(x) = -6, indicating that the function is concave down and decreasing in this interval.
   • For x > 1, f”(x) = 6, indicating that the function is concave up and increasing in this interval.

Therefore, we conclude that the function f(x) = x^3 – 3x^2 + 2x is concave down and decreasing for x < 1, and concave up and increasing for x > 1.

Example 2:

Let’s consider the function g(x) = -2x^2 + 4x – 1 and determine if it is increasing or decreasing based on the second derivative test.

1. Find the second derivative of the function: g”(x) = -4.
2. Simplify the derived expression: g”(x) = -4.
3. Since the second derivative is a constant, there are no inflection points.
4. Choose test points within each interval: x = 0 and x = 1.
5. Evaluate the second derivative at the test points: g”(0) = -4 and g”(1) = -4.
6. Analyze the signs of the second derivative in each interval:
   • Since the second derivative is always negative (-4), the function is concave down and decreasing in the entire domain.

Therefore, we conclude that the function g(x) = -2x^2 + 4x – 1 is concave down and decreasing for the entire domain.

By working through these example problems, we gain practical experience in applying the second derivative test to determine if a function is increasing or decreasing based on the concavity of the function. Remember to verify your answers with additional tests and analysis if needed.

Conclusion

In this article, we have explored two powerful methods for determining if a function is increasing or decreasing: the first derivative test and the second derivative test. These tests allow us to analyze the behavior of functions and gain valuable insights into how they change as their input values vary.

By using the first derivative test, we can evaluate the sign of the derivative to determine if a function is increasing or decreasing. This method provides a straightforward approach to analyzing the behavior of the function at critical points and in various intervals.

The second derivative test takes our analysis a step further by examining the concavity of the function. By evaluating the sign of the second derivative, we can identify whether a function is concave up or concave down, providing additional information about the function’s curvature and behavior.

Both tests are essential tools in understanding the behavior of functions in finance and other fields. By knowing whether a function is increasing or decreasing, we can make informed decisions based on trends, market behavior, and investment performance.

Remember to follow the step-by-step processes outlined in this article when applying these tests to functions. By finding the derivatives, simplifying expressions, identifying critical points or inflection points, and evaluating test points, we can confidently determine the intervals where a function is increasing or decreasing.

Throughout this article, we have explored example problems illustrating the application of the first derivative test and the second derivative test. By practicing with these problems, you can enhance your understanding and ability to analyze functions effectively.

Now that you have a solid foundation in determining if a function is increasing or decreasing, you can apply these techniques to various financial scenarios and make more informed decisions based on the behavior of functions.