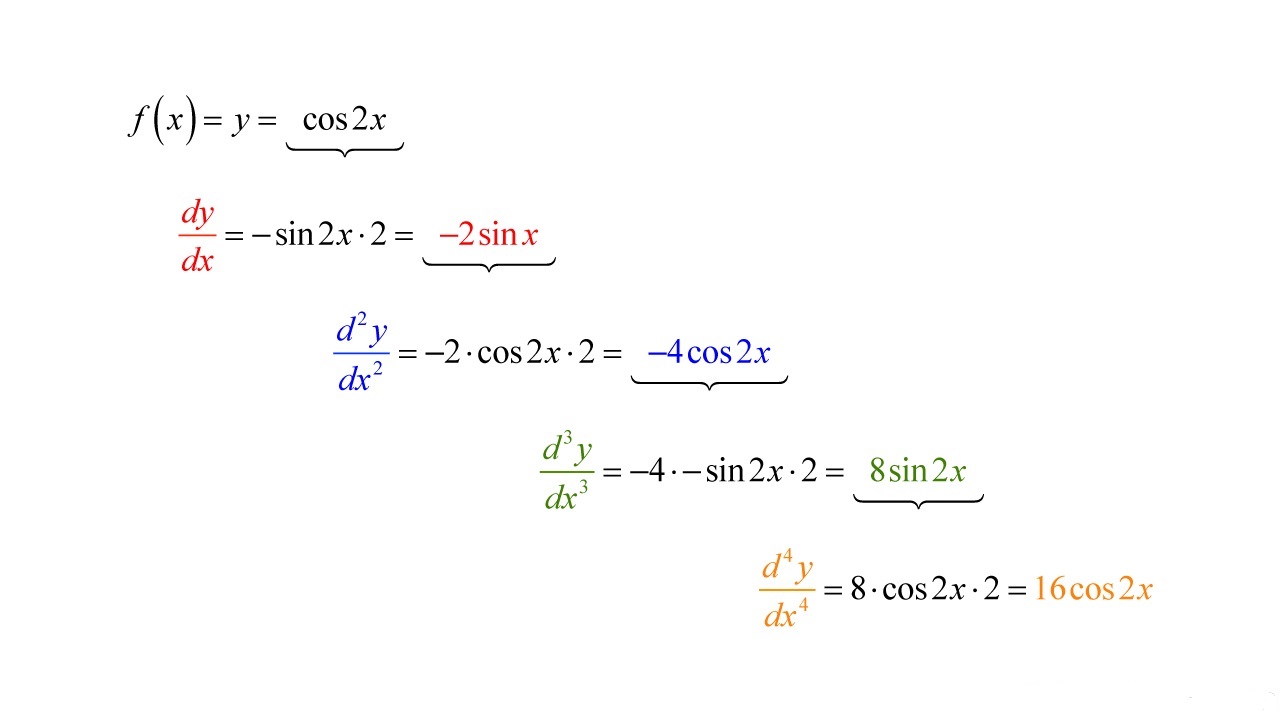How To Remember Derivatives Of Trig Functions

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for LiveWell, at no extra cost. Learn more)

Introduction

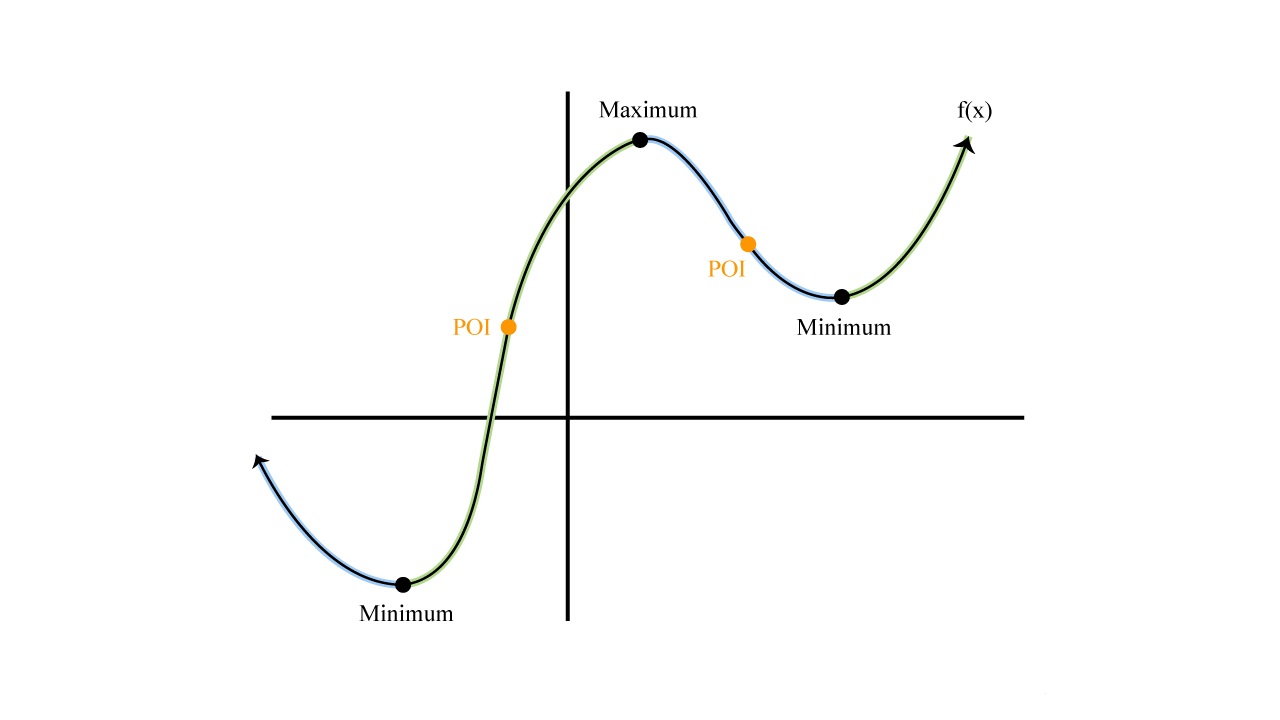
Trigonometry is the study of the relationships between angles and the sides of triangles. It plays a crucial role in various disciplines, including physics, engineering, and finance. Understanding trigonometric functions and their derivatives is fundamental when it comes to solving complex mathematical problems.

In this article, we will focus on how to remember the derivatives of trigonometric functions. Derivatives are a mathematical concept that represents the rate of change of a function at a given point. Knowing the derivatives of trigonometric functions allows us to find the slope of curves, analyze the behavior of functions, and solve optimization problems.

Learning the derivatives of trigonometric functions can be challenging, as it requires memorization of specific formulas and rules. However, by breaking down the concepts and using mnemonic techniques, remembering the derivatives becomes much more manageable.

Whether you are a student studying calculus or a professional working with complex mathematical models, having a solid understanding of the derivatives of trigonometric functions can greatly enhance your problem-solving abilities.

In the following sections, we will explore the derivatives of various trigonometric functions in detail, providing mnemonic devices and examples to help you remember them effectively.

Basic Trigonometric Functions

Before diving into the derivatives of trigonometric functions, let’s review the basic trigonometric functions that form the foundation of this topic.

The three fundamental trigonometric functions are sine (sin), cosine (cos), and tangent (tan). These functions relate the angles of a right triangle to the ratios of its sides.

• Sine (sin): The sine of an angle is equal to the ratio of the length of the side opposite the angle to the length of the hypotenuse.
• Cosine (cos): The cosine of an angle is equal to the ratio of the length of the adjacent side to the length of the hypotenuse.
• Tangent (tan): The tangent of an angle is equal to the ratio of the length of the side opposite the angle to the length of the adjacent side.

These functions are periodic, repeating their values after every 360 degrees or 2π radians. They have various applications, such as analyzing periodic phenomena, solving triangles, and modeling oscillatory behavior.

Now that we have refreshed our understanding of the basic trigonometric functions, let’s move on to the derivatives of these functions, which will allow us to analyze their rates of change and explore more complex mathematical concepts.

The Power Rule

The power rule is a basic rule of calculus that allows us to find the derivative of a function raised to a power. This rule is essential when it comes to finding the derivatives of trigonometric functions.

The power rule states that if we have a function of the form f(x) = x^n, where n is a constant, then the derivative of f(x) with respect to x is f'(x) = n * x^(n-1).

When applying the power rule to trigonometric functions, we can rewrite them as f(x) = sin^m(x), f(x) = cos^m(x), or f(x) = tan^m(x), where m is a constant exponent. To find the derivative of these trigonometric functions, we can simply apply the power rule.

For example, let’s find the derivative of f(x) = sin^3(x). We can rewrite this function as f(x) = (sin(x))^3. Applying the power rule, we have f'(x) = 3 * (sin(x))^2 * cos(x).

Similarly, we can find the derivatives of functions like f(x) = cos^4(x) and f(x) = tan^2(x) by applying the power rule.

The power rule is a fundamental tool in calculus and is widely used in deriving and analyzing various mathematical functions. By understanding and mastering this rule, we can simplify the process of finding derivatives and make our calculations more efficient.

The Chain Rule

The chain rule is another crucial rule in calculus that allows us to find the derivative of composite functions. A composite function is a combination of two or more functions, where the output of one function becomes the input of another.

When dealing with trigonometric functions, it is common to encounter composite functions. For example, consider a function like f(x) = sin(2x). Here, we have the sine function nested inside another function, which is 2x. To find the derivative of this function, we need to apply the chain rule.

The chain rule states that if we have a composite function of the form f(g(x)), where f is the outer function and g is the inner function, then the derivative of f(g(x)) with respect to x is given by f'(g(x)) * g'(x).

Applying the chain rule to our example, we have f(x) = sin(2x), and the outer function is f(u) = sin(u), where u = 2x. The derivative of the outer function is f'(u) = cos(u). The inner function is g(x) = 2x, and its derivative is g'(x) = 2. Therefore, using the chain rule, we find that the derivative of f(x) = sin(2x) is f'(x) = cos(2x) * 2.

The chain rule allows us to handle more complex functions by breaking them down into simpler components and finding their individual derivatives. By understanding and applying this rule, we can efficiently compute the derivatives of composite trigonometric functions.

It is important to note that when applying the chain rule, we may encounter more intricate composite functions involving multiple trigonometric functions. In such cases, it is crucial to carefully identify the inner and outer functions and apply the chain rule step by step.

Derivatives of the Sine Function

The sine function, denoted as sin(x), is one of the fundamental trigonometric functions. It represents the ratio of the length of the side opposite an angle in a right triangle to the length of the hypotenuse. The derivative of the sine function plays a significant role in calculus, as it allows us to analyze the rate of change of sine functions and solve various mathematical problems.

The derivative of the sine function can be found using the chain rule. Let’s consider the derivative of sin(x). By applying the chain rule, we have d/dx(sin(x)) = cos(x). This means that the derivative of the sine function is equal to the cosine function. The cosine function represents the rate of change of the sine function with respect to the angle.

For example, if we have a function f(x) = sin(2x), where the angle is multiplied by a constant 2, we can find its derivative. Using the chain rule, we differentiate the outer function sin(u) with respect to u, where u = 2x, and then multiply it by the derivative of the inner function 2x. Therefore, we find that the derivative of f(x) = sin(2x) is f'(x) = cos(2x) * 2 = 2cos(2x).

The derivative of the sine function provides valuable information about the behavior of periodic phenomena and oscillatory systems. It allows us to study the amplitude, frequency, and phase shifts of such functions. Additionally, the derivative of the sine function is utilized in various fields, including physics, engineering, and signal processing, to analyze and manipulate waveforms.

Remembering the derivative of the sine function as cos(x) is essential when solving calculus problems involving trigonometric functions. By understanding the relationship between the sine and cosine functions, we can navigate through complex mathematical operations and obtain meaningful results.

Derivatives of the Cosine Function

The cosine function, denoted as cos(x), is another fundamental trigonometric function that relates the ratio of the length of the adjacent side to the length of the hypotenuse of a right triangle. Understanding the derivatives of the cosine function is essential in calculus, as it allows us to analyze the rate of change of cosine functions and solve various mathematical problems.

Similar to the derivative of the sine function, the derivative of the cosine function can be found using the chain rule. Let’s consider the derivative of cos(x). By applying the chain rule, we have d/dx(cos(x)) = -sin(x). This means that the derivative of the cosine function is equal to the negative of the sine function. The sine function represents the rate of change of the cosine function with respect to the angle.

For example, if we have a function f(x) = cos(3x), where the angle is multiplied by a constant 3, we can find its derivative. By applying the chain rule, we differentiate the outer function cos(u) with respect to u, where u = 3x, and then multiply it by the derivative of the inner function 3x. Therefore, we find that the derivative of f(x) = cos(3x) is f'(x) = -sin(3x) * 3 = -3sin(3x).

The derivative of the cosine function provides valuable information about the behavior of periodic phenomena and oscillatory systems, just like the sine function. It helps analyze the amplitude, frequency, and phase shifts of such functions. The derivative of the cosine function is widely used in physics, engineering, and signal processing, where the manipulation and analysis of waveforms are crucial.

Remembering the derivative of the cosine function as -sin(x) is important when dealing with calculus problems involving trigonometric functions. Understanding the relationship between the cosine and sine functions allows us to effectively navigate through complex mathematical operations and arrive at meaningful solutions.

Derivatives of the Tangent Function

The tangent function, denoted as tan(x), is a trigonometric function that represents the ratio of the sine of an angle to the cosine of the same angle. Understanding the derivatives of the tangent function is crucial in calculus, as it allows us to analyze the rate of change of tangent functions and solve various mathematical problems.

To find the derivative of the tangent function, we can use the quotient rule. The quotient rule states that if we have a function of the form f(x) = g(x) / h(x), then the derivative of f(x) with respect to x is given by f'(x) = (h(x) * g'(x) – g(x) * h'(x)) / (h(x))^2.

Now, let’s consider the derivative of the tangent function. We have f(x) = tan(x) = sin(x) / cos(x). By applying the quotient rule, we can find the derivative of f(x). The derivative of the numerator sin(x) is cos(x), and the derivative of the denominator cos(x) is -sin(x). Hence, using the quotient rule, we find that the derivative of f(x) = tan(x) is f'(x) = (cos(x) * cos(x) – sin(x) * (-sin(x))) / (cos(x))^2 = sec^2(x), where sec(x) stands for the secant function.

The derivative of the tangent function, which is sec^2(x), represents the rate of change of the tangent function with respect to the angle. It is used in various mathematical applications, such as solving optimization problems and analyzing trigonometric functions.

Remembering the derivative of the tangent function as sec^2(x) is crucial in calculus when dealing with trigonometric functions. By understanding this relationship, we can effectively compute the derivatives of tangent functions and incorporate them into our mathematical calculations and analyses.

Derivatives of the Cosecant Function

The cosecant function, denoted as csc(x), is the reciprocal of the sine function. It represents the ratio of the hypotenuse to the side opposite an angle in a right triangle. Understanding the derivatives of the cosecant function is essential in calculus, as it allows us to analyze the rate of change of cosecant functions and solve various mathematical problems.

To find the derivative of the cosecant function, we can use the chain rule. Let’s consider the derivative of csc(x). By applying the chain rule, we have d/dx(csc(x)) = -csc(x) * cot(x). This means that the derivative of the cosecant function is the negative cosecant function multiplied by the cotangent function.

The cotangent function, denoted as cot(x), represents the ratio of the cosine of an angle to the sine of the same angle. By understanding the relationship between the cotangent, cosecant, sine, and cosine functions, we gain insights into various trigonometric identities and their derivatives.

For example, if we have a function f(x) = csc(2x), where the angle is multiplied by a constant 2, we can find its derivative. By applying the chain rule, we differentiate the outer function csc(u) with respect to u, where u = 2x, and then multiply it by the derivative of the inner function 2x. Therefore, we find that the derivative of f(x) = csc(2x) is f'(x) = -csc(2x) * cot(2x) * 2 = -2csc(2x) * cot(2x).

Understanding the derivatives of the cosecant function and its relationship with the cotangent function is important in calculus when dealing with trigonometric functions. By mastering these concepts, we can effectively analyze the rate of change and behavior of cosecant functions, enabling us to solve a wide range of mathematical problems.

Derivatives of the Secant Function

The secant function, denoted as sec(x), is the reciprocal of the cosine function. It represents the ratio of the hypotenuse to the length of the adjacent side in a right triangle. Understanding the derivatives of the secant function is essential in calculus, as it allows us to analyze the rate of change of secant functions and solve various mathematical problems.

To find the derivative of the secant function, we can use the chain rule. Let’s consider the derivative of sec(x). By applying the chain rule, we have d/dx(sec(x)) = sec(x) * tan(x). This means that the derivative of the secant function is the secant function multiplied by the tangent function.

The tangent function, denoted as tan(x), represents the ratio of the sine of an angle to the cosine of the same angle. By understanding the relationship between the secant, tangent, sine, and cosine functions, we gain insights into various trigonometric identities and their derivatives.

For example, if we have a function f(x) = sec(3x), where the angle is multiplied by a constant 3, we can find its derivative. By applying the chain rule, we differentiate the outer function sec(u) with respect to u, where u = 3x, and then multiply it by the derivative of the inner function 3x. Therefore, we find that the derivative of f(x) = sec(3x) is f'(x) = sec(3x) * tan(3x) * 3 = 3sec(3x) * tan(3x).

Understanding the derivatives of the secant function and its relationship with the tangent function is important in calculus when dealing with trigonometric functions. By mastering these concepts, we can effectively analyze the rate of change and behavior of secant functions, enabling us to solve a wide range of mathematical problems.

Derivatives of the Cotangent Function

The cotangent function, denoted as cot(x), is the reciprocal of the tangent function. It represents the ratio of the cosine of an angle to the sine of the same angle. Understanding the derivatives of the cotangent function is crucial in calculus, as it allows us to analyze the rate of change of cotangent functions and solve various mathematical problems.

To find the derivative of the cotangent function, we can use the chain rule. Let’s consider the derivative of cot(x). By applying the chain rule, we have d/dx(cot(x)) = -csc^2(x). This means that the derivative of the cotangent function is the negative cosecant squared function.

The cosecant function, denoted as csc(x), is the reciprocal of the sine function. By understanding the relationship between the cotangent, cosecant, and sine functions, we can derive the derivative of the cotangent function.

For example, if we have a function f(x) = cot(2x), where the angle is multiplied by a constant 2, we can find its derivative. By applying the chain rule, we differentiate the outer function cot(u) with respect to u, where u = 2x. Therefore, we find that the derivative of f(x) = cot(2x) is f'(x) = -csc^2(2x).

Understanding the derivatives of the cotangent function and its relationship with the cosecant function is important in calculus when dealing with trigonometric functions. By mastering these concepts, we can effectively analyze the rate of change and behavior of cotangent functions, enabling us to solve a wide range of mathematical problems.

It is worth noting that the derivative of the cotangent function can also be derived using the quotient rule, considering it as the ratio of cosine and sine functions. However, using the relationship with the cosecant function provides a more concise and straightforward approach.

Summary and Key Points

Understanding the derivatives of trigonometric functions is essential in calculus and various fields of mathematics and science. Let’s summarize the key points we have covered so far:

• The derivatives of trigonometric functions can be found using rules such as the power rule and the chain rule.
• The power rule allows us to find the derivative of a function raised to a power.
• The chain rule is used to find the derivative of composite functions, where one function is nested inside another.
• The derivative of the sine function, sin(x), is the cosine function, cos(x).
• The derivative of the cosine function, cos(x), is the negative sine function, -sin(x).
• The derivative of the tangent function, tan(x), is the secant squared function, sec^2(x).
• The derivative of the cosecant function, csc(x), is the negative cosecant function multiplied by the cotangent function, -csc(x) * cot(x).
• The derivative of the secant function, sec(x), is the secant function multiplied by the tangent function, sec(x) * tan(x).
• The derivative of the cotangent function, cot(x), is the negative cosecant squared function, -csc^2(x).

By understanding and mastering these derivative rules and relationships, we can efficiently compute the derivatives of trigonometric functions and apply them to solve a wide range of mathematical problems. Additionally, these concepts provide insights into periodic phenomena, oscillatory systems, and waveforms, making them valuable tools in various scientific and engineering disciplines.

Remembering and practicing these derivative rules will strengthen your mathematical skills and open doors to more advanced areas of calculus. By consistently applying these rules and understanding their significance, you will enhance your problem-solving abilities and gain a deeper appreciation for the power and beauty of trigonometric functions.